Summary

In EMSolution, electromagnetic force calculations are performed using the nodal force method (Refs. [1,2]). The nodal force method is based on integrating the Maxwell stress tensor with the gradient of the nodal shape function, which represents virtual displacements, to obtain the force at the nodal point. The Maxwell stress tensor is clear for air and linear magnetic materials, but there are many theories about nonlinear magnetic materials.

Explanation

In EMSolution, the expression for the Maxwell tensor

$$T_{ij} = H_{i}B_{j}-\delta_{ij} \int_{0}^{H}B \cdot dH$$

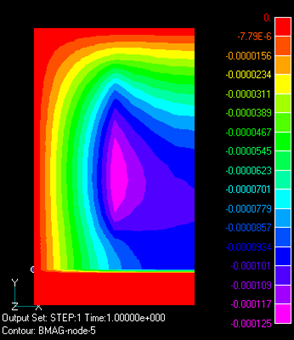
is adopted. If the tensor is not symmetrical, such as magnets, we use a symmetrized version. However, this formula can be used for nonlinear materials without hysteresis, but in the case of hysteresis and anisotropic materials, it is questionable. The above integral is the so-called magnetic field co-energy (with respect to energy). For magnets, the above integral is currently replaced by $\frac {B・H}{2}$. In the literature [3], it is expressed as $\frac {B・H}{2}$ in all cases. In a magnetic body, there is coupling with the mechanical stress field, and it may be difficult to separate the electromagnetic stress from the mechanical stress. What kind of expression formula should be used for electromagnetic stress is an issue for the future. In general, for objects with uniform magnetic permeability, such as air, electromagnetic forces appear only on their surfaces. Also, the overall electromagnetic force or torque acting on a rigid body will be the same no matter how the Maxwell stress tensor is assumed within the magnetic body. It may be assumed to be zero. This is because when the object is moved without deformation, there is no change in energy within the object, and the electromagnetic force or torque is determined solely by the distribution of the magnetic field around the object. The so-called Maxwell stress method, which determines the force or torque by integrating the Maxwell stress on the surface of the air region around the object, uses this property. The situation is exactly the same for the nodal force method. Now, as an example, consider the model shown in Fig. 1. The analysis is a translational two-dimensional calculation. Suppose that a magnet magnetized to 1T is on a magnetic plate $（m_r=1000）$. If the boundary conditions are set as shown in Fig. 1, we can simulate the case where the magnets are aligned with alternating polarity. The magnetic plate should be pulled upward. The magnetic flux distribution is shown in Fig. 2. There is almost no magnetic field leakage below the magnetic plate. The magnetic flux distribution in the magnetic plate is as shown in Fig. 3. The arrow points to the left and is almost uniform in the thickness direction. Since this is a linear material, the magnetic field is higher than $10 T$. In reality, saturation occurs and this is not possible, but please understand that this is a conceptual discussion.

Fig.1 Analysis model

Fig.2 Magnetic flux distribution

Fig.3 Magnetic flux density distribution in magnetic plate

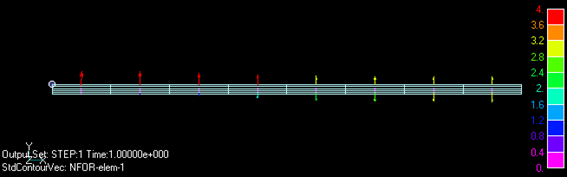
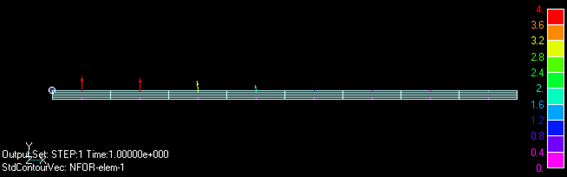
The forces acting on the magnetic plate obtained by the nodal force method are shown in Figs. 4 and 5. The nodal forces are converted to forces acting on the elements. In Fig. 4, the Maxwell stresses in the magnetic material shown in the introduction are used, and in Fig. 5, no electromagnetic stresses from within the magnetic material are assumed. The total upward force is exactly the same, but the distribution is very different. What stands out in Fig. 4 is the reverse direction force acting on the upper and lower surfaces on the right side of the figure. This is due to the strong magnetic field along the planes inside the magnetic body, which causes the expansion force. In Fig. 5, the force disappears and becomes a force that pulls the top surface upward; Fig. 5 looks more intuitively reasonable.

Fig.4 The forces acting on the magnetic plate obtained by the nodal force method (Considering Maxwell stress in the magnetic material)

Fig.5 The forces acting on the magnetic plate obtained by the nodal force method (Neglecting Maxwell stress in the magnetic material)

References

[1] A. Kameari, “Local force calculation in 3D FEM with edge elements”,　International Journal of Applied Electromagnetics in Materials 3, 1993, pp. 231-240.
[2] A. Kameari, “Electromagnetic Force Analysis by Nodal Force Method”, IEEJ　Joint Study Group on Static and Rotating Machines Materials, SA-93-11, RM-93-49, 1993.
[3] Isao Imai, “Thinking about Electromagnetism”, Science Inc., 1992.

Download

・ input
・ pre_geom2D.neu : Mesh file