Summary

Conductivity is known to be temperature-dependent, and we have added the new function to analyze using temperature-dependent conductivity. Eddy current analysis can be performed by setting the conductivity-temperature curve and the temperature of element or property.

Explanation

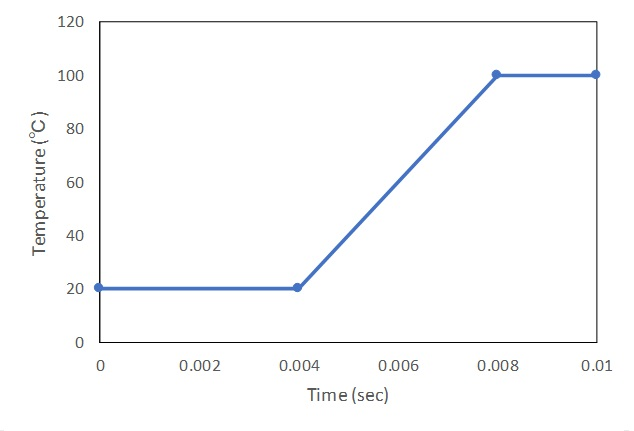
his function is illustrated using a model simulating a bifurcated conductor as shown in Fig. 1, which was used in the "DC Current Field Analysis of Bulk Conductors". The two bifurcations have the same geometry, but the conductivity at one side is smaller than the other, assuming that the temperature rises on that side. Fig. 2 shows the temperature vs. conductivity curve used in the analysis. Please note that the temperature rise is assumed to be very short, but this is for sample calculations.
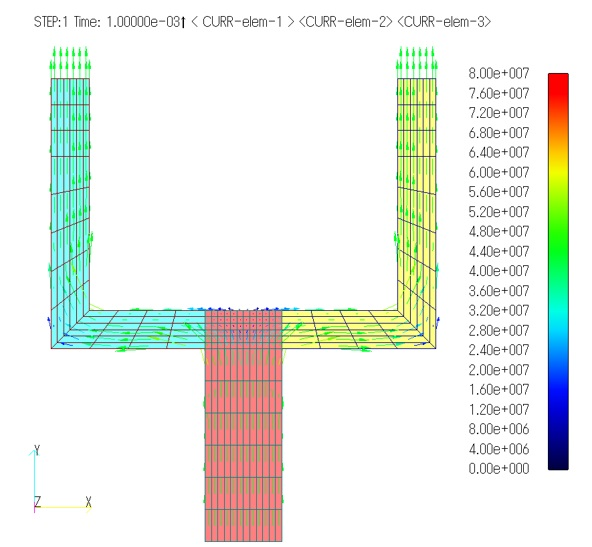
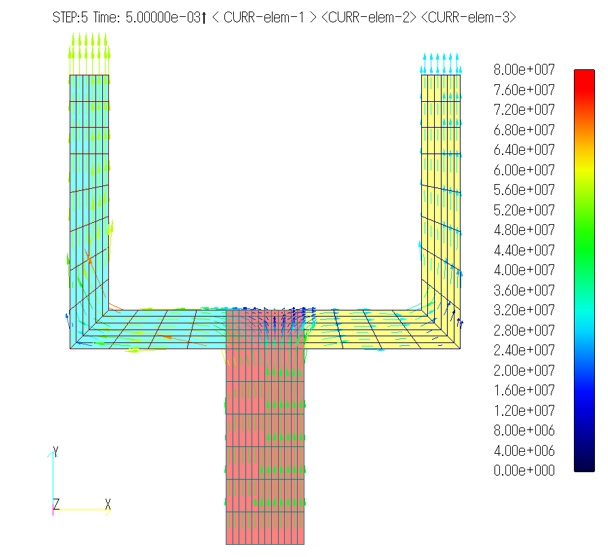
Fig.3 shows the current distribution at times 0.001s, 0.005s, and 0.01s. You can see that the left branch is gradually approaching a steady state because the conductivity does not change, while the right branch, on the contrary, shows a decrease in current due to the change in conductivity. The temperature-dependent conductivity analysis function uses interpolation from the conductivity-temperature curve. The temperature can be specified on an element-by-element or property-by-property basis, and the temperature at each time must be set in a separate file "temperature.dat".

Fig.1 Bifurcated conductor model
(excluding air region)

Fig.2 Temperature variation with time

(a) 0.001 sec.

(b) 0.005 sec.

(c) 0.010 sec.

Fig.3 Current density vector distribution ($A/m^2$)

Briefly, we have introduced an analysis that takes into account the temperature dependence of conductivity. This function can be used for transient analysis of bulk conductors using SUFCUR. It can also be used for "steady-state current field analysis" (Handbook "2. Types of Analysis"). Basically, conductivity-temperature curves are used, but may also be used when conductivity depends on factors other than temperature.

How to use

The TEMP_DEPEND module is required to use the temperature-dependent conductivity analysis function.

* STATIC * STEP * AC * TRANSIENT * DISPLACEMENT * NON_LINEAR * TEMP_DEPEND * STEADY_CURRENT * 0 0 0 1 0 0 1 0

Set the ID of the temperature-dependent conductivity curve described below to the new option SIGMA_DEPEND_ID in Handbook "16.1.1 Element Volume Characteristics". If SIGMA_DEPEND_ID>0, the value of SIGMA is not used.

* MAT_ID * POTENTIAL * BH_CURVE_ID * SIGUMA * MU * PACKING * ANISOTROPY * IRON_LOSS * SIGMA_DEPEND_ID * 1 0 0 1e+008 1 1 0 0 1

The conductivity-temperature curve would be set to the new NO_SIGMA_DEPENDENT_CURVES.

• CURVE_ID：Conductivity-temperature curve ID

• NO_DATA：Number of data points

• TYPE=0：Default

• TEMPERATURE：Temperature (℃)

• SIGMA：Conductivity ($S/m$)

  The temperature for each element is specified in temperature.dat. The version number at the beginning of the input file must be "r12.0" or higher.

• NO_STEP：Number of steps to set temperature

• TYPE=0：Temperature is set for each element.
  　　=1：Temperature is set for each property.

• NO_DATA：Number of elements to be set for TYPE=0, number of properties to be set for TYPE=1

• INPUT_TYPE=0： Fixed

• FORMAT =0：Set in the format described below.
  　　　　=1：Set in ATLAS format; only used in case of TYPE=0.

• REDIRECT=0：Output the contents of temperature.dat to the check file.
  　　　　=1：Do not output to the check file.

• IDS：Element number (TYPE=0) or property number (TYPE=1)

• TIME：Time, to be set to include the computed time of the input file.

• IDS：Temperature （℃）

* NO_SIGMA_DEPENDENT_CURVES * 1 * CURVE_ID * NO_DATA * TYPE * 1 6 0 * TEMPERATURE * SIGMA * 0 1e+008 20 1e+008 40 5e+007 60 5e+007 80 2.5e+007 100 2.5e+007

Download

Bifurcated conductor model　　Sample data DL

・ input3D_SUFCUR_tempDepend.ems
・ pre_geom2D.neu
・ 2D_to_3D
・ temperature.dat