Summary

When using the sliding method, the accuracy of the mesh data can have a significant impact. In particular, problems arise when the nodal positions on both sides of the period facing the sliding surface do not exactly match the period; the ICCG method does not converge and diverges, or converges but does not provide a reasonable solution. A simple example is shown below.

xplanation

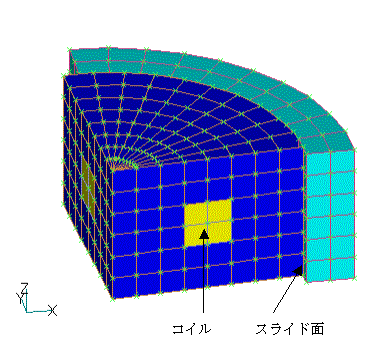
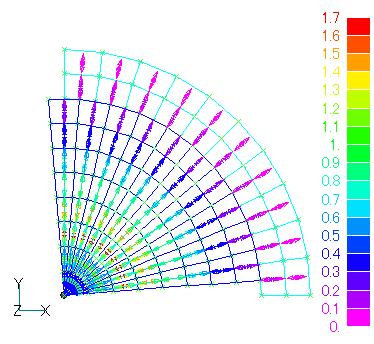
As shown in Fig. 1, there is an axisymmetric coil with air on the outside. The air region is divided by a slide plane, and the interior is rotated by 5 degrees (half of the mesh in the direction of rotation). A normal calculation results in an axisymmetric magnetic field as shown in Fig. 2. Viewed from above, the result would look like Fig. 3, showing that the magnetic field is axisymmetric.

Fig.1 Analysis model

Fig.2 Magnetic flux density distribution

Fig.3 Magnetic flux density distribution, projected from above

If we force the analysis to use a mesh with the nodal position on one side shifted by 0.1 degree, as shown in Fig. 4, the magnetic field will be as shown in Fig. 4. The convergence of the ICCG method is shown in Fig. 5. When the node is moved, convergence is also achieved, but the convergence is not smooth and the number of iterations is high.

Fig.4 Magnetic flux density distribution in question

Fig.5 Convergence of ICCG method

As described above, if the periodic symmetry position is not in a precise symmetrical position, convergence will be poor and the results will not be valid. The cause is that the amount of magnetic flux is not balanced between the fixed and movable parts. This problem can be avoided by entering a value of about 0.1 for the FITNESS parameter of the sliding surface if the meshes are equally spaced in the direction of movement and the analysis is performed when the meshes overlap, as in this example. However, this is not applicable when the meshes are located in the middle of each other.

For larger meshes, the conditions seem to be more stringent. When creating a mesh, there is bound to be some positional error, but even that can cause problems. In this case, the significant digits are also important, and the higher the accuracy, the better the convergence. By changing the output from 8 to 12 significant digits in the FEMAP nerutral file format and increasing the number of significant digits in the EMSolution input, we have achieved convergence from $10^{-4}$ to There is an example of convergence up to $10^6$ and a reasonable solution was obtained. To increase the number of significant digits of input in EMSolution, set the input parameter WIDE to 1 or 2.

If the meshes converge well when they overlap on the sliding surface, but do not converge when they reach intermediate positions, this may be the cause. In the case of a motion analysis of a moving part, a situation such as this would occur, so sufficient accuracy is required in the mesh data.
As mentioned above, ensuring the accuracy of nodal coordinates is a major burden in mesh creation, so starting with EMSolution r9.7.8, the program forcibly replaces symmetrically located nodes with equal ones and aligns them with the one with the smaller periodic coordinates. This will be reflected in post_geom.