Summary

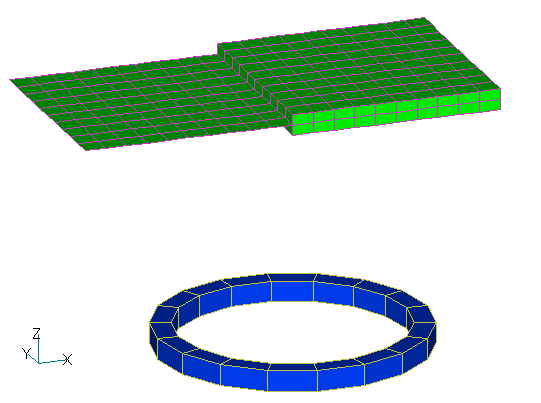
EMSolution provides non-magnetic thin plate elements. It is applicable to non-magnetic conductor plates whose thickness is sufficiently small compared to the skin thickness and is defined as a face element. Modeling with three-dimensional solid elements slows down the convergence of the ICCG method because of the very flat elements, but this is not the case with non-magnetic thin plate elements. Another advantage is that meshing becomes easier.

Explanation

Previously, electromagnetic forces acting on non-magnetic thin plate elements were only calculated using the nodal force method, but we are pleased to report that we have added a function to calculate the Lorentz force ($J x B$). Nonmagnetic thin plate elements have a magnetic field in the vertical direction as an attribute, but they do not have a magnetic field in the in-plane direction, and the in-plane direction magnetic field is discontinuous at the top and bottom of the plane. For this reason, the calculation was difficult, and the development was delayed. However, the in-plane component magnetic field in a plane element is obtained by obtaining the in-plane magnetic fields in the upper and lower planes from solid elements that are in contact with the upper and lower planes and averaging them. A simple example of the calculation is shown below to evaluate its validity. As shown in Fig. 1, the analytical model is a half of a square plate, with one side ($x > 0$) modeled by a solid element and the other side ($x < 0$) by a face element. Assume that both have the same equivalent thickness. A magnetic field is applied with a circular coil, and the resulting eddy currents and electromagnetic forces in the conducting plate are calculated. The analysis is performed at a sufficiently low frequency of $10 Hz$ AC steady-state analysis.

Fig.1 Analysis model

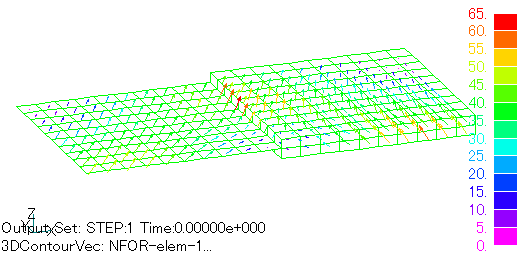
Fig. 2 shows the eddy current distribution at phase zero obtained by the analysis. Fig. 3 shows the electromagnetic force density distribution obtained by the nodal force method, and Fig. 4 shows the electromagnetic force density distribution due to Lorentz force, which is a newly added function. The nodal force method and the Lorentz force method are in good agreement on the plane element side.

Fig.2 Eddy Current Density Distribution [$N/m^2$]

Fig.3 Electromagnetic force density distribution [$N/m^3$] by nodal force method

Fig.4 Electromagnetic force density distribution [$N/m^3$] by Lorentz force method

Next, the analytical results of the integrated force in each region are shown.
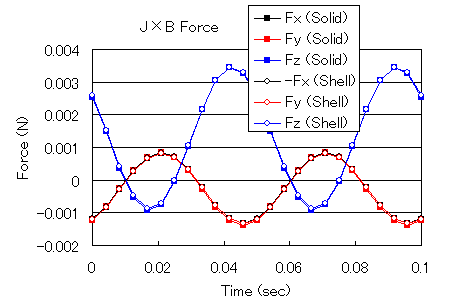
Figs. 5 and 6 show the time variation of the integrated force in each direction on the solid element side and the face element side using the nodal force method and Lorentz force method, respectively. The agreement between the two is good, and the symmetry between the solid side and the face element side is also good. In other words, we can see the relationship Fx(Solid)=-Fx(Shell), Fy(Solid)=Fy(Shell), and Fz(Solid)=Fz(Shell). Fx on the face element side is shown with positive and negative values reversed for easy comparison.

Fig.5 Time variation of the total electromagnetic force by nodal force method

Fig.6 Time variation of the total electromagnetic force due to Lorentz force

The electromagnetic force acting on the coil is calculated by the new function "COIL (external current magnetic field source)". The force acting on the conductor and the force acting on the coil are in an action-reaction relationship and should be equal in the opposite direction, which is also the case in the calculation results.

Fig.7 Time variation of the total z-directional electromagnetic force acting on COIL

As described above, the analytical results of the electromagnetic force by Lorentz force are in good agreement with those by the nodal force method and are reasonable. Although the Lorentz force and the electromagnetic force by the nodal force method should agree with each other in non-magnetic conductors, there are many cases where the agreement is not good due to numerical errors. We believe that the surface element approximation can be used to compare the two, which may be useful in examining the accuracy of the electromagnetic force. In addition, when there is a weak magnetic field fluctuation in a strong magnetic field, the nodal force may not be accurate. Electromagnetic force due to nodal force may be calculated even in static magnetic fields where it should not appear. In such cases, the Lorentz force is considered more appropriate. For more information on the relationship between Lorentz force and nodal force, please click here.

How to use

The output of electromagnetic force due to Lorentz force for non-magnetic thin plate elements can be the same as for conventional solid elements. Flag FORCE_J_B in the output file FORCE_J_B in "Handbook 10. Input/Output Files" to output the electromagnetic force for non-magnetic thin plate elements. For the element quantity, setting FORCE_J_B=1 will output the element integral force (N), and setting FORCE_J_B=2 will output the volumetric electromagnetic force density ($N/m^3$) (please note that the volume density is used to match units with solid elements). The nodal quantity is the Lorentz force converted to nodal force, in N. This nodal force is for nodal force in stress analysis and can be used directly for stress analysis. For printout, set FORCE_J_B=1 in 11. Printout to output the Lorentz force summation for each physical property of the non-magnetic thin plate element.

Download

・ input
・ pre_geom.neu