Summary

Generally, embedded permanent magnet type rotating machines (IPM motors) are operated with field weakening control by increasing the current advance angle in order to reduce the induced voltage due to the magnet flux at high speeds, taking advantage of their characteristics. If the magnetic flux generated by the armature winding is too large, the operating point of the permanent magnet may exceed the knee point, resulting in irreversible demagnetization.
In actual motor design, the operating point is often determined to prevent irreversible demagnetization, so we have created a function to calculate the permeance coefficient by post-processing. This allows the possibility of irreversible demagnetization to be shown. It also calculates the rate of decrease from the input (initial) magnetization to the operating point, taking into account the demagnetizing field.

Starting with EMSolution r12.0.3, nonlinear analysis including irreversible demagnetization can be handled. For details, see "Demagnetization Analysis of Permanent Magnets".

Explanation

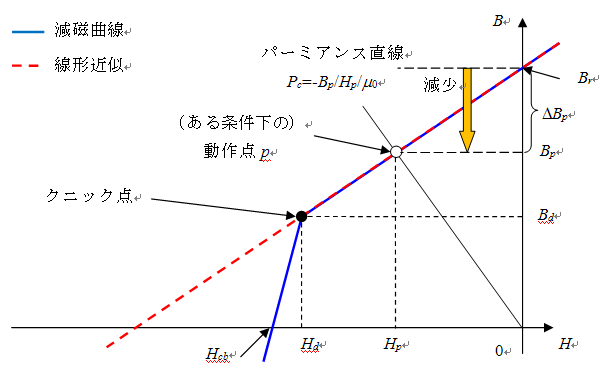
Here, the rate of decrease from the input magnetization to the operating point and the permeance coefficient are defined as follows:

• Rate of decrease from input magnetization to operating point
  The rate of decrease from the input magnetization ($B_r$)
  to the operating point ($B_d$ [T]) is expressed as $(B_r – B_d)/B_r$.

• Permeance coefficient
  The permeance coefficient is expressed as $−B_d / H_d/ μ_0$ in terms of $B_d$ [T] and $H_d$ [A/m] at the operating point. It is an index to determine if the operating point has fallen below the knee point.

An image of demagnetization by demagnetizing field is shown in Fig. 1. Since EMSolution treats the magnet as a linear material, the operating point moves on the red dotted line. Under certain conditions, the magnetic flux density $B_p$ at the operating point p is less than the input magnetization $B_r$, and the rate of reduction is defined as ($\Delta B_p$)/$B_r$. Considering that demagnetization is caused by the reverse magnetic field, the rate of decrease is 100% when the external magnetic field is equal in magnitude and opposite in direction to $B_r$, i.e., when $\Delta B_p = B_r$. In the case of a knee point, the actual demagnetization curve will change as shown by the blue line. For the permeance coefficient, a large permeance coefficient is equivalent to a small rate of decrease. Therefore, based on the coefficient of permeance at the knee point, it is possible to indicate whether or not there is a possibility of irreversible demagnetization by checking whether the coefficient of permeance is lower than the coefficient of permeance at the knee point.

Fig.1 Demagnetization curve, operating point, cnic point and permeance coefficient (image)

Based on the above idea, we have prepared a function to calculate the permeance coefficient and the rate of decrease from the input magnetization to the operating point in the post-processing of EMSolution.

Analysis example

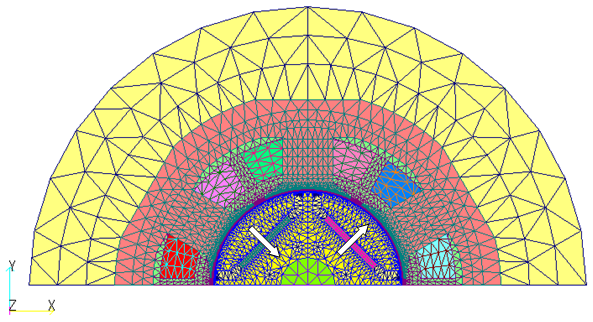
An example of calculating the rate of decrease from the input magnetization to the operating point and permeance coefficient using the D1 model, an IEEJ benchmark motor, is shown in Fig. 2. Note that all analyses are two-dimensional.Table 1 summarizes the calculation conditions for permanent magnets.

Table1 Calculation conditions for permanent magnets

Fig.2 Verification model D1 model

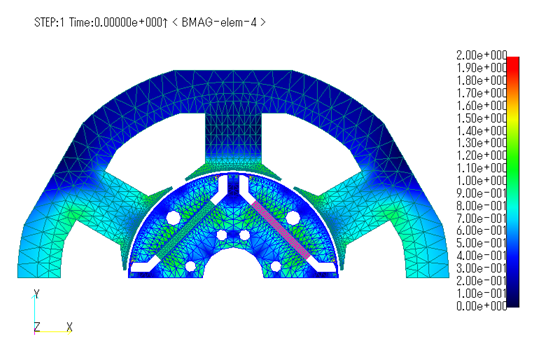
First, the results of the no-load operation analysis are shown. Fig. 3 shows the magnetic flux density distribution at the first step, and Figs. 4 and 5 show the maximum rate of decrease from the input magnetization to the operating point and the minimum permeance coefficient at one cycle of the electric angle. A decrease rate of 1 from the input magnetization to the operating point means 100% reduction. Due to the formation of the magnetic circuit, the reduction is small, with a maximum reduction of about 21%.

Fig.3 Magnetic flux density distribution in the first step [T] (No-load operation)

Fig.4 Maximum rate of decrease distribution from input magnetization
to operating point for one cycle of electric angle (No-load operation)

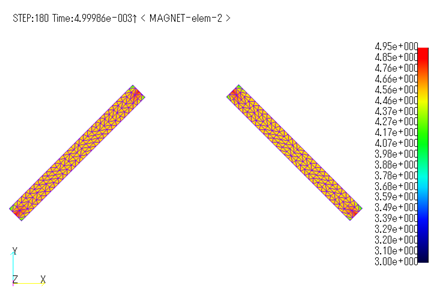
Fig.5 Distribution of the minimum permeance coefficient
for one cycle of electric angle [H] (No-load operation)

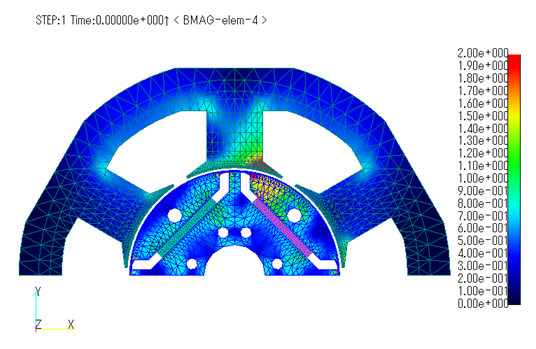
Next, the results are shown for a field weakening condition with a speed of 6000 $min^{-1}$, armature current of 7.5 Arms, and current advance angle $\beta$ = 60deg. Fig. 6 shows the magnetic flux density distribution at the first step, and Figs. 7 and 8 show the maximum rate of decrease from the input magnetization to the operating point and the minimum permeance coefficient at one cycle of the electric angle, respectively. Since the magnetic flux is generated by the coil in the direction that cancels the magnet flux chained to the coil, a demagnetizing field is applied to the magnet, and the maximum decreasing rate from the input magnetization to the operating point is larger than in the no-load operation condition, with a maximum reduction rate of about 42%. For example, if the no-load operation analysis is used as the reference for the operating point, the demagnetization ratio is the difference of the decreasing ratio between the field weakening operation and the no-load operation.

Fig.6 Magnetic flux density distribution diagram of the first step [T]
(Field weakening operation)

Fig.7 Maximum rate of decrease distribution from input magnetization
to operating point for one cycle of electric angle (Field weakening operation)

Fig.8 Distribution of the minimum permeance coefficient
for one cycle of electric angle [H] (Field weakening operation)

From the above, we can show the possibility of demagnetization without executing irreversible demagnetization analysis.

How to use

This calculation is done by post-processing (set POST_PROCESSING = 1).

* PRE_PROCESSING * MAKE_SYSTEM_MATRICES * 　　　 　 0 0 * SOLVE_EQUATION * POST_PROCESSING * 　　　 　 0 1

When MAGNETIZATION = 2, the distribution of the rate of decrease from the input magnetization to the operating point is output to MAGNET-elem-1 in the magnetization file, and the permeance coefficient ( H ) is output to MAGNET-elem-2, respectively, as elemental quantities. It also outputs the distribution of the maximum rate of decrease and minimum permeance coefficient for one cycle when AVERAGE = 1.

* POST_DATA_FILE * ELEM_OUT * NODE_OUT * NUMBER_OUTPUT_MATS * AVERAGE * WIDE * SUF_OPTION * 5 1 0 0 1 0 0 * MESH * CURRENT * MAGNETIC * FORCE_J_B * FORCE_NODAL * DISP * ELEM * HEAT * MAGNETIZATION * 0 0 0 0 0 0 0 0 　 　　 2

Download

D1 model (concentrated winding IPM motor) sample data DL

• Mesh data：
  • pre_geom2D.neu (Stator mesh)
  • rotor_mesh2D.neu (Rotor mesh)
• No load operation:
  • input2D_static_6000rpm_p2.ems
    (Static field analysis for initial values)
  • input2D_transient_6000rpm_p2.ems
    (Transient analysis)
  • inputPost2D_demag_transient_6000rpm_p2.ems
    (Post-processing for calculating this function)
• Field weakening operation：
  • input2D_static7.5A60deg_p2.ems
    (Static field analysis for initial values)
  • input2D_transient7.5A60deg_p2.ems
    (Transient analysis)
  • inputPost2D_demag_transient7.5A60deg_p2.ems
    (post-processing for performing this function)

Note: When performing transient analysis calculations, rename the "solutions" file calculated in the static field analysis for initial values to the "old_solutions" file and place it in the same folder.