Summary

NETWORK and CIRCUIT are two methods for considering connections to electrical circuits in EMSolution. NETWORK is considered intuitive and easy to understand because it uses the circuit elements and power sources described in the circuit diagram and their connections as input data. CIRCUIT, on the other hand, organizes the circuit connections into only independent variables and gives the connections as matrices, which is like directly representing the circuit equations to be solved. Therefore, CIRCUIT is not suitable for very complex calculations, partly because of the difficulty in creating input data. However, since NETWORK is an optional module, you may want to use only CIRCUIT for simple circuits.
Therefore, we will explain the correspondence between NETWORK and CIRCUIT using a commonly used three-phase circuit as an example.

Explanation

NETWORK

NETWORK is a method of describing circuit elements and their connections from a schematic to an EMSolution input and is considered easy to understand because it is intuitive. Therefore, we will first show the circuit diagram of the model to be calculated and create data using NETWORK in order to make an easy-to-understand comparison with CIRCUIT. Fig. 1 shows the schematic of a three-phase circuit. The blue letters in the figure indicate element numbers, and the red letters indicate terminal numbers. This circuit is the one connected to the “Modeling of unipolar squirrel-cage induction motor” and you can download the mesh, input files, etc. The orange part in Fig. 1 represents the coil, which is divided into elements and subjected to magnetic field analysis using the finite element method. The part of the circuit that is in series with each phase is called a branch, and each branch is referred to as Branch 1, Branch 2, and Branch 3. Hereafter, the subscripts for elements, power supplies, etc. correspond to the respective branch numbers. The resistance ($r_1$,$r_2$,$r_3$), self-inductance ($l_1$,$l_2$,$l_3$), and mutual inductance ($m_{12}$,m_{23}$,$m_{31}$) of the coils modeled in the mesh are taken into account within EMSolution, so the user need not specify these values. (Inductor resistance can also be given as part of the external resistance, without being calculated by EMSolution).

Next, external resistors (R1, R2, R3), external self-inductances (L1, L2, L3), and external mutual inductances (M12, M23, M31), such as external elements and cables not included in the finite element mesh model, are represented as NETWORK resistance elements R, inductance elements L, and mutual inductance elements M. Also, the constant-voltage power supply is set as the voltage source element VPS and the constant-current power supply is set as the current source element CPS. A constant-voltage power supply VPS is used here, and V1, V2, and V3 give the three-phase voltage conditions for the U, V, and W phases with equal magnitudes and phase delays of 120° in that order. Therefore, equation (1) holds.

$$\begin{array}{r}\begin{array}{l}{\displaystyle V1=V{e}^{j\omega t}}\\ {\displaystyle V2=V{e}^{j(\omega t–2\pi /3)}}\\ {\displaystyle V1+V2+V3=0}\end{array}\} (1)\end{array}$$

The NETWORK data are set in the input file as shown in Fig. 2. However, external self and mutual inductance are not considered, and all coil resistances of the mesh model are assumed to be $2.92\mathrm{\Omega }$ as external resistance R. The rotor bar resistance is calculated inside EMSolution by giving the conductivity of the rotor bar as $1.01\times {10}^{7}S/m$ and defining it in SUFCUR. the bottom two lines of Fig. 2 are the circuit of the rotor bar, which is not directly related to the three-phase circuit, and the rotor bar power supply is the constant-current power supply CPS, whose magnitude is 0. This connection to a constant current source CPS of magnitude 0 represents that the circuit is short-circuited, i.e., current is conserved.

Fig. 3 shows the time function given to a constant-voltage power supply, including its magnitude and phase over time. The voltage magnitude is V (≈81.649 V), which is the maximum value obtained by converting the line voltage of 100 V to phase voltage, the period is 0.2 s (frequency 50 Hz), and the phase is 0, -120, and -240 degrees at t=0 for phases U, V, and W, respectively.

Contrasting with the variables in Fig. 1, we see that equation (2) holds:

$$\begin{array}{r}\begin{array}{l}{\displaystyle R_1=R_2=R_3=2.92}\\ {\displaystyle L_1=L_2=L_3=M_{12}=M_{23}=M_{31}=0}\\ {\displaystyle V_1=81.649e^{j\omega t}, V_2=81.649e^{j(\omega t–2\pi /3)}, V_3=81.649e^{j(\omega t–4\pi /3)}}\end{array}\} (2)\end{array}$$

$I_1$, $I_2$, and $I_3$ are unknown variables, but since it is a three-relative circuit, the following equation holds:

$${\displaystyle I_1=I_2=I_3=0 (3)}$$

Although the constant supply voltage is given as three-phase input data, the obtained analysis results generally show that the currents are not necessarily three-phase. For example, the mesh geometry of the “Modeling of unipolar squirrel-cage induction motor”, which is also an example of this analysis, is not symmetrical with respect to the three phases, so the internal inductances are not equal and $I_1$, $I_2$, and $I_3$ are not symmetrical.
Perform a linear ac steady-state analysis (AC). Since the model is an induction machine, material nonlinearity and the effects of slip frequency and slot harmonics would normally appear in the current waveform, but since this is an AC analysis, the results are obtained assuming the material is linear. The results for the output circuit element at t=0 are shown in Fig. 4.

**************************************************************************** * Step No. 1 Time 0.0000000000e+00 sec * **************************************************************************** *** Network elements ***************************************************** ID No. Current Voltage Flux 1 -3.03495e+00 7.30453e+01 -1.63183e-02 2 2.94163e+00 -3.19766e+01 2.07350e-01 3 9.33242e-02 -4.02936e+01 -1.94012e-01 4 -3.03495e+00 8.86207e+00 5 2.94163e+00 -8.58956e+00 6 9.33242e-02 -2.72507e-01 7 3.03495e+00 8.16490e+01 8 -2.94163e+00 -4.08245e+01 9 -9.33242e-02 -4.08245e+01

Fig.4 NETWORK output (time portion)

The ID No. in Fig. 4 corresponds to the element number in blue in Fig. 1. 1 to 3 are the coils of the mesh, 4 to 6 are the external resistors, and 7 to 9 are the power supplies, representing the current and voltage phase difference flowing through each. 1 to 3 also show the amount of magnetic flux chained to the coils. This is the amount of magnetic flux chained in the coil per number of turns, as explained in “Handling of inductance in external current field source (COIL)”. It can be seen that the conditional equations (1) and (3) for the current and the voltage of the power supply are all satisfied. Although not shown here, results other than $t\ne 0$ are satisfied as well.

CIRCUIT

CIRCUIT is a method of setting up independent closed loops without treating the schematic as it is in NETWORK. As is well known, the number of independent closed loops is the number of co-trees in graph theory. Since the number of independent closed loops in the circuit shown in Fig. 1 is 2, we define closed loops A and B as shown in Fig. 5, and let the currents flowing in each loop be the closed circuit currents $I_A$ and $I_B$. Then the following determinant relationship is established between the branch currents $I_1$, $I_2$, and $I_3$ defined in NETWORK and the closed loop currents $I_A$ and $I_B$.

$$\left\{\begin{array}{c}{I}_1\\ I_2\\ I_3\end{array}\right\}=\left[\begin{array}{cc}1& 0\\ 0& 1\\ -1& -1\end{array}\right]\left\{\begin{array}{c}{I}_A\\ I_B\end{array}\right\} (4)$$

Similarly, the following determinant relationship holds for the voltages $V_1$, $V_2$, and $V_3$ of each branch power supply defined by NETWORK and the voltages $V_A$ and $V_B$ of the closed loop power supplies.

$$\left\{\begin{array}{c}{V}_A\\ V_B\end{array}\right\}=\left[\begin{array}{ccc}1& 0& -1\\ 0& 1& -1\end{array}\right]\left\{\begin{array}{c}{V}_A\\ V_B\\ V_C\end{array}\right\} (5)$$

The matrix representing the relationship between the branch and the closed loop expressed in equation (5) is called the closed path matrix or the tieset matrix. As can be seen from equations (4) and (5), the matrix representing the relationship between the branch and the closed-loop current and voltage is a transpose matrix.

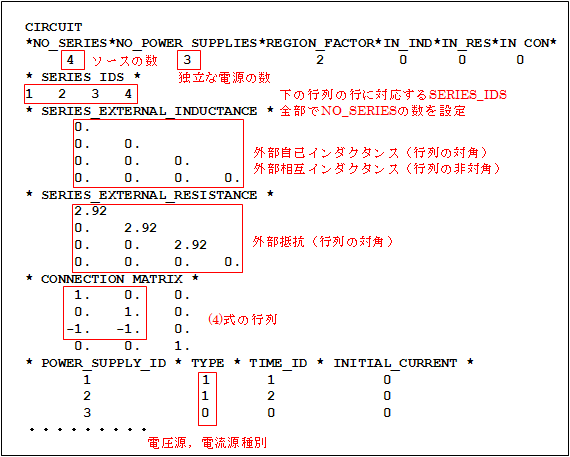
Fig. 6 shows the CIRCUIT settings. External resistance and inductance are entered as matrices. The number of sources is set in NO SERIES, and the number of independent sources is set as POWER SUPPLIES. Also, set the connection matrix in equation (4) as CONNECTION MATRIX.

Since the voltages $V_A$ and $V_B$ are the input values for the closed-loop voltages in equation (5), we show how to find them; Fig. 7 shows the vectors of the branch voltages $V_1$, $V_2$, and $V_3$, which are the three relative nominal voltages. From equation (5), for example, $V_A$ is $V_1-V_3$, so the vector is $\sqrt{3}$ times larger than $V_1$ in magnitude and 30 degrees behind $V_1$ in phase, as shown by the red arrow. Similarly, $V_B$, indicated by the blue arrow, is $\sqrt{3}$ times larger than $V_1$ in magnitude and lags 90 degrees behind $V_1$ in phase. Thus, as shown in Fig. 8, the magnitude of the voltage is $100\sqrt{2}V$. This is equivalent to converting the Y-connection to a $\mathrm{\Delta }$-connection and then to a V-connection with one edge removed to make it a closed circuit. Note that the negative sign on the magnitude is due to the reverse definition of the direction of the constant-voltage power supply in NETWORK.

As in the NETWORK case, an AC analysis was performed and the results for the output circuit at t=0 are shown in Fig. 9.

**************************************************************************** * Step No. 1 Time 0.0000000000e+00 sec * **************************************************************************** *** Sources ********************************************************* ID No. Amplitude(Current) Voltage Flux 1 -3.03498e+00 -8.19080e+01 -1.63184e-02 2 2.94165e+00 4.05665e+01 2.07351e-01 3 9.33253e-02 4.05665e+01 -1.94014e-01 4 0.00000e+00 3.43931e-06 -2.08027e-08 *** Power Sources *************************************************** ID No. Current Voltage 1 -3.03498e+00 -1.22474e+02 2 2.94165e+00 -8.65956e-15 3 0.00000e+00 3.43931e-06

Fig.9 CIRCUIT output

ID No. 1, 2 and 3 of Sources in Fig.9 represent Branch 1, Branch 2 and Branch 3, respectively. Amplitude (Current) is the branch currents $I_1$, $I_2$, and $I_3$, corresponding to the currents of ID No. 1, 2, and 3 in Fig. 3. Voltage represents the voltage drop outside the power supply of each branch as shown in Fig. 4. For example, the Voltage of Branch 1 is $-8.19080e+001V$ from Fig. 9, which corresponds to the sum of ID Nos. 1 and 5 of NETWORK. ID Nos. 1 and 2 of Power Sources in Fig. 9 represent closed loops A and B, respectively. Current is the closed-circuit current $I_A$, $I_B$, and Voltage represents the power source for each closed loop as shown in Fig. 4. For example, we can see that the Voltage of ID No. 1 of CIRCUIT is $-1.22474e+002V$, which matches the sum of ID Nos. 7 and 9 of NETWORK.
We hope you now understand the relationship between NETWORK and CIRCUIT in a three-phase circuit. Whether you set up a NETWORK or a CIRCUIT, please simulate the circuit you are assuming. As indicated in the text, the data used here can be found in “Analysis of Induction Motors” for CIRCUIT and “Handling of Rotor Bars and End Rings in Two-Dimensional Analysis of Squirrel-cage Induction Motor” and “Modeling of Unipolar Squirrel-cage Induction Motor” for the NETWORK setting method.