Summary

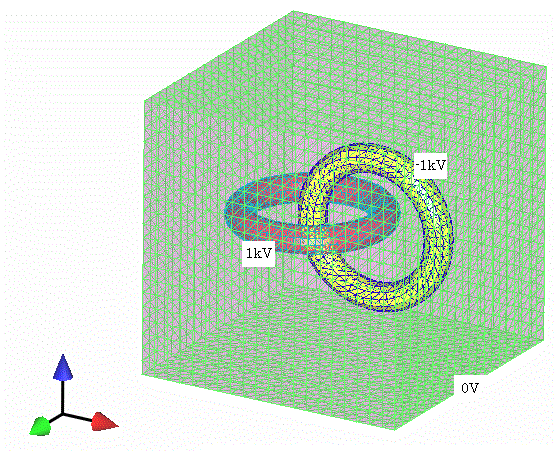
As an example of a three-dimensional analysis, consider the model shown in Fig. 1, although it is not realistic.

Explanation

Suppose two conductor rings are placed inside a cubic conductor box. The two rings are chained together and one ring is charged to 1kV and the other to -1kV. Assume that the conductor box is grounded and has a potential of 0. As for the mesh, the inside of the ring is hollow, with face elements defined on the surface. The mesh inside the box consists of tetrahedrons. The tetrahedral division of the interior was done using FEMAP’s automatic division function.

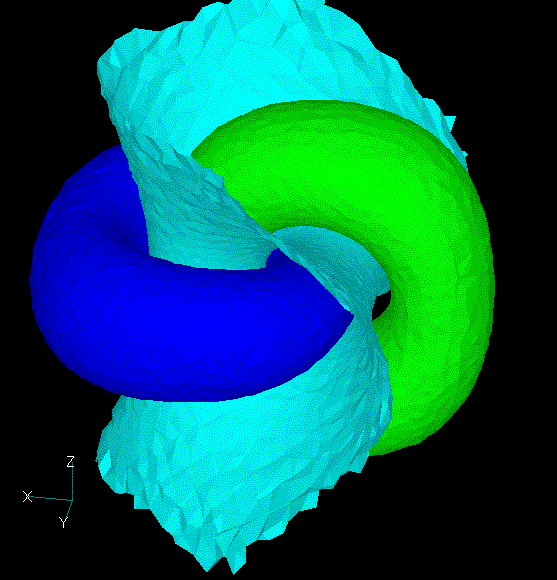
Fig. 2 shows the electric field intensity distribution on the surface of the ring. Figs. 1 and 2 are displayed using a viewer created using Java3D. Fig. 3 shows the equipotential surface of the space, which is displayed using FEMAP.

EMSolution’s electrostatic field analysis is a similar procedure to conventional magnetostatic field analysis. In electrostatic field analysis, the surface of the conductor that gives the potential (which can also give the amount of charge) must be defined by a surface element and included in the mesh data. Also, for solid elements, instead of specific permeability, specific permittivity should be entered. The boundary condition can be a zero potential surface or a surface where the electric field is parallel to the surface. Periodic boundary conditions can also be imposed in the same way as in magnetic field analysis.

The boundary conditions are problematic as an open domain problem, and it is difficult to perform a high-precision electric field analysis using finite element method, but if you are interested in trying a simple electric field analysis using finite element method, please feel free to use it.

Fig.1 Three-dimensional electrostatic field analysis model

Fig.2 Electric field strength distribution on ring surface

Fig.3 Equipotential iso-surface diagram

Download

Analysis Model

・ input
・ pre_geom.neu