Summary

In EMSolution, we have provided various functions to handle the magnetic properties of magnetic materials. For example, “Analysis of Nonlinear Two-Dimensional Anisotropic Magnetic Properties” shows an analysis method that takes into account direction-dependent magnetic properties, such as anisotropic electromagnetic steel sheets. In addition, the paper “Analysis of laminated iron core by homogenization method” shows how to approximate and calculate objects that are not homogeneous at the microscopic level, such as laminated steel sheets, as homogeneous materials. Furthermore, “Calculation of Iron Loss by Post-Processing” shows a method for evaluating iron loss.
In recent years, it is required to calculate iron loss as accurately as possible when developing low-loss electric devices. In the iron loss evaluation method by post-processing described above, the iron loss can be easily calculated by approximating the magnetic property by initial magnetization curve, but for more accurate calculation, it is important to use an analysis method that directly considers the effect of hysteresis of magnetic materials. In this situation, we have developed a hysteresis analysis function that applies the hysteresis model, the Play model, to EMSolution.

Explanation

1. Play model

Although many modeling approaches have been proposed to express hysteresis magnetic characteristics, we have adopted the Play model, which has recently attracted much attention. The Play model is represented by a simple operator called hysteron, which delays the phase of the output relative to the input. Fig. 1 shows the operating characteristics of the play hysteron. The hysteron is represented by a simple equation as in equation (1), which is equivalent to the behavior of a two-cart model as shown in Fig. 2. In equation (1), $\zeta$ is the hysteron width, $B$ is the magnetic flux density, $p$ is the hysteron, and $p_0$ represents the past hysteron. The play model is obtained by preparing hysterons of various $\zeta$, acting on each hysteron with a function called the shape function, and taking the sum of all the hysterons.

$$p_{\zeta}(B) = B-\frac{\zeta(B-p^{0})}{max(|B-p^{0}_{\zeta}|)}$$

Fig. 3 shows the hysteresis curve of an electromagnetic steel sheet equivalent to 50A470, expressed using the Play model. Since the Play model is a mathematical model based on measured data, it requires measured data in a specified format. Since the accuracy of the measured data may affect the accuracy of the magnetic field analysis and the nonlinear convergence characteristics, it is necessary to devise ways to improve the accuracy of the data. Since the play model calculation is performed using the shape function derived from the measured data, the shape function has to be identified from the measured data prior to the magnetic field calculation. We will show how to do this in the next issue.

Since the Play model is a model that expresses DC magnetic properties, and the shape function is identified from DC magnetization properties that do not include the effects of eddy currents, in the analysis model with a fluctuating magnetic field, the conductivity is set as input data for EMSolution as before, and the eddy current field is solved.

2. Hysteresis analysis using ring samples

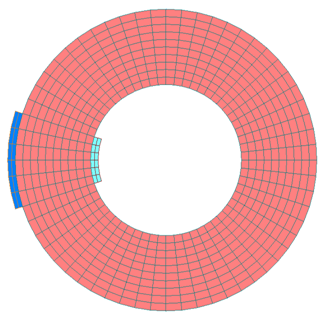
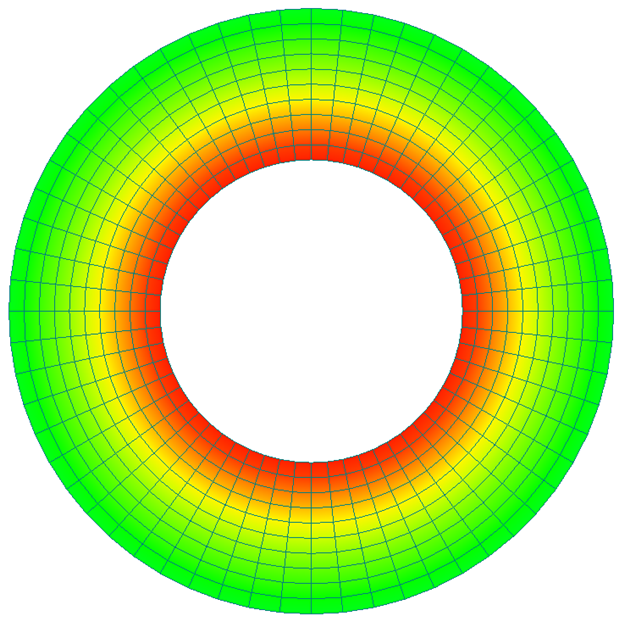
Hysteresis analysis is performed using the ring sample shown in Fig. 4. The analysis is performed with the mesh data, pre_geom2D.NEU, and the analysis condition file input. The shape function file required for the play model analysis is shape.
If eddy currents in the sample are neglected, the analysis becomes a two-dimensional static analysis, but the component of the magnetic field in the radial direction of the sample is small, so the model is in fact a one-dimensional model. Since there are no voids in the ring sample and no magnetic poles appear, it can be said to be an analysis model in which the effects of hysteresis are noticeable. As initial conditions, the ring sample is assumed to be demagnetized and a sinusoidal current of 0.05 $Hz$ and a maximum of 5 $AT$ is applied to the coil.

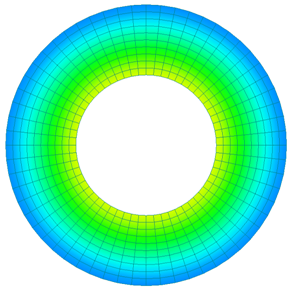
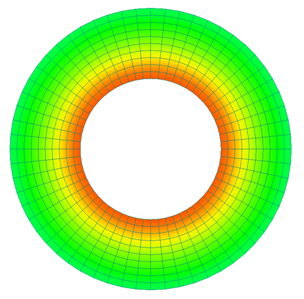
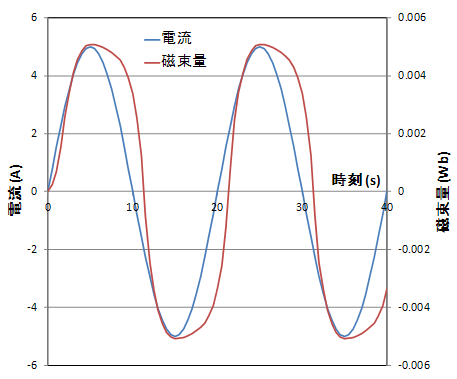
Fig. 5 shows the temporal variation of the magnetic flux density distribution. As can be seen from the figure, the magnitude of the current at (a) 2.5s when the current increases and (c) 7.5s when the current decreases are equal, but the magnetic flux density distribution is different because the ring is magnetized. Fig. 6 shows the time variation of the current flowing in the coil and the amount of magnetic flux linkage to the coil. It can be seen that the phase of the magnetic flux quantity lags behind the current, which is qualitatively correct.

Please refer to the references for further explanation. However, the hysteresis material and other factors are different from those in the text.

3. Hysteresis loss distribution

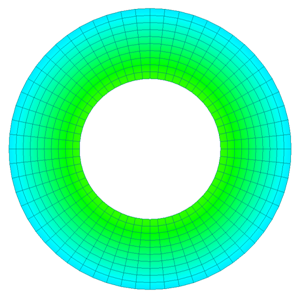
Similar to the “Iron Loss Calculation by Post-processing”, the hysteresis loss distribution of a hysteresis analysis using Play model can be output as post data. The hysteresis loss distribution for the ring sample model described above is shown in Fig. 7(a). The iron loss is evaluated not in the first period starting from the initial state of no-excitation, but in the period after the second period when a steady state is reached. Fig.7(b) shows the hysteresis loss distribution calculated in “Iron loss calculation by post-processing” (calculation method ②). Fig. 8 graphs the results of each calculation method as distribution values in the radial direction. In the post-processing iron loss calculation, the hysteresis loss changes in proportion to the square of the magnetic flux density, but in the Play model calculation, the loss is calculated according to the hysteresis characteristics actually measured. The hysteresis characteristics used in the Play model calculations are based on actual measurements, but the iron loss coefficients in the post-processing were obtained from the manufacturer’s catalogs.

How to use

1. Setting up hysteresis analysis

Since the element coefficient matrix is asymmetric in the hysteresis analysis using Play model, the asymmetric solver is set up in MATRIX_ASYMMETRICITY (Handbook Section 3.2.6).

* TREE GAUGE * REGLARIZATION * SCALING * LINE SEARCH * MATRIX ASYMMETRICITY * -1 0 0 1 　1

Set ANISOTROPY=5 (Handbook section 16.1.1) to indicate that this is a magnetic material to which the Play model is applied. In the next line, enter the global or local coordinate system COORDINATE_ID, the specific magnetic permeability MU_Z in the Z direction, the calculation width of the magnetic flux density DB_CAL ( T ), and the material identification number PLAY_ID of shape.
Note that hysteresis analysis using the PLAY model always requires shape file with shape function data representing hysteresis characteristics. A smaller DB_CAL generally results in higher accuracy, but at the expense of computation time per nonlinear iteration. To reduce the computation time, the option DB_FACTOR > 1 is available, which increases DB_CAL by a factor of DB_FACTOR until the nonlinear convergence condition ( NON_LINEAR_CONV or CHECK_B < 0 ) converges, thereby reducing the computation time per nonlinear iteration. Finally, after the convergence judgment is made, DB_CAL is set back to the input value again for convergence. Note that this option is not used here.

* MAT_ID * POTENTIAL * B_H_CURVE_ID * SIGMA * MU * PACKING * ANISOTROPY * IRON_LOSS * 1 0 0 0.0 1000 0 5 0 * COORDINATE_ID * MU_Z * DB_CAL * PLAY_ID * DB_FACTOR * 0 1.0 0.001 1 1.0

2. Setting hysteresis loss distribution data

Next, we will explain how to output hysteresis loss distribution data. Although it is possible to output the data at the time of the main calculation described above, it is usually calculated as a post-processing step since it is a cycle-by-cycle process. For post-processing, set PRE_PROCESSING, MAKING_MATRICES, and SOLVING_EQUATION in Handbook “1. Execution Control” to 0 and set only POST_PROCESSING to 1.

* PRE_PROCESSING * MAKE_SYSTEM_MATRICES * 0 0 * SOLVE_EQUATION * POST_PROCESSING * 0 1

To calculate the iron loss for one cycle, set STEP_INTERVAL in Handbook “9. Output Steps, Phase” to the number of steps for one cycle.

* INITIAL_STEP * LAST_STEP * STEP_INTERVAL * 41 80 40

When calculating hysteresis loss distributions using the Play model, set IRON_LOSS(11)=3 (Handbook “11.1 Output Options”). And specify the output unit IRON_LOSS(10)=2 (Handbook “10.2 Output Files”). Note that specifying IRON_LOSS(10)=1 will not output anything in the post data.

* POST_DATA_FILE * ELEM_OUT * NODE_OUT *NUMBER_OUTPUT_MATS * AVERAGE * 5 1 1 0 1

For your reference, the settings for post-processing iron loss calculations are also shown below. The method below is also used when calculating eddy current losses using eddy current loss coefficients in hysteresis analysis with the Play model. Set IRON_LOSS(11)=2 when using the calculation method ②.

* MESH * CURRENT * MAGNETIC * FORCE_J_B * FORCE_NODAL * DISP * ELEM * HEAT * MAGNETIZATION * IRONLOSS * 0 0 0 0 0 0 0 0 0 2 * MESH * A * V * B * B_INTEG * J_Q * 0 0 0 0 0 0 * Q_AVERAGE * HEAT * MAG_FLUX * CUR_FLUX * 0 0 0 0 * FORCE_J_B * FORCE_NODAL * MAGNETIC_ENERGY * IRON_LOSS * 0 0 0 2

Then, set IRON_LOSS(16)=1 (Handbook “16.1.1 Volume Element Properties”) for iron loss calculation by post-processing, then enter density ($kg/m^3$), eddy current loss coefficient KE ($W/kg/T^2/Hz^2$), and hysteresis loss coefficient KH ($W/kg/T^2/Hz$).

* MAT_ID * POTENTIAL * B_H_CURVE_ID * SIGMA * MU * PACKING * ANISOTROPY * IRON_LOSS * 1 0 1 0 1 1 0 0 * COORDINATE_ID * MYU_Z * DB_CAL * PLAY_ID * DB_FACTOR * 0 1.0 0.001 1 1.0 * COORDINATE_ID * MASS_DENSITY * KE * KH * 0 7.70E+03 1.37E-04 2.60E-02

Output file contents: in case of FEMAP Neutral file format

< When calculating hysteresis loss using the Play model >

iron_loss:

LOSS-elem-1　Hysteresis loss （$W/m^3$）
LOSS-elem-2　Anomalous eddy current loss　（$W$）

< When calculating iron loss by post-processing >

iron_loss:

LOSS-elem-1　Anomalous eddy current loss　（=1：$W/kg$ 　or　 =2：$W/m^3$）
LOSS-elem-2　Anomalous eddy current loss　（$W$）
LOSS-elem-3　Hysteresis loss（=1：$W/kg$ 　or 　=2：$W/m^3$）
LOSS-elem-4　Anomalous eddy current loss　（$W$）

Output list (output file) contents

*************************************************************** * Average from Step No.4 to Dtep No.8 Period 2.00000e+001 sec * ←　Integration time *************************************************************** 　・ 　・ *************************************************************** * Total iron loss in regions (PlayModel) * *************************************************************** MAT No. hysteresis loss(W) 1 1.5805E-03 ←　Hysteresis loss occurring during integration time Total 1.5805E-03 　　（loss per unit time [$W$]）

Ahagon, Kameari: “Examination of Hysteresis Analysis by Finite Element Method Using Isotropic Vector Play Model,” IEEJ Joint Workshop on Stationary and Rotating Equipment, SA-09-67, RM-09-73 (2009)

Download

Ring Sample Data　　Sample data DL
・ input.ems
・ pre_geom2D.neu
・ shape

Iron loss calculation data by post-processing　　Sample data DL
・ input_iron_loss2
・ input_iron_loss3