Summary

EMSolution has a function to obtain the magnetic field at an arbitrary spatial point by volume integrating the magnetization in the element. However, it should be noted that the calculation accuracy of the magnetic field is deteriorated when trying to obtain the magnetic field near a magnetic element using this function. As an example, we will examine the accuracy of the analysis of the magnetic field of a uniformly magnetized rectangular body. Note that this model has an analytical solution and can be compared with the true value.

Explanation

Suppose a 0.2 $\times$ 0.2 $\times$ 0.2m magnetic material is uniformly magnetized at 1T in the z direction as shown in Fig. 1. However, due to symmetry considerations, we have analyzed the 1/8 region. Since the magnetization is constant and known, a finite element analysis is not required, and the magnetic field in space can be obtained simply by integrating the magnetization of the magnetic body elements.

Fig.1 Analytical model magnetic flux density distribution

Fig. 2 shows the relative error of the magnetic field of the numerical solution with different orders of Gaussian integration of the elements compared to the analytical solution without numerical integration (true value) in the vicinity of the magnetic material on the z-axis. Note that the vertical axis is on a logarithmic scale. To obtain an accuracy of 1% or better, integrations of 7th order or better are required for z = 0.101m (1/10 of the element size from the magnetic surface), 5th order or better for z = 0.102m (1/5 of the element size), 3rd order or better for z = 0.105m (1/2 of the element size), and 1st order or better for z = 0.11m (1 of the element size). The number of integration points in the element is the cube of the Gaussian integral order, and the calculation time is proportional to the number of integration points.

Fig.2 Accuracy of magnetic field integration on z-axis

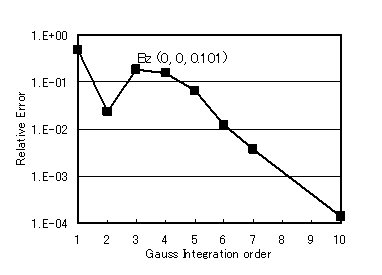
Fig. 3 shows the dependence of the relative error on the order of integration at z=0.101 m. Above 5th order, the error is almost inversely proportional to the order power. Although the error is low at the second order, it is considered to be dependent on the location of the evaluation point and cannot be said to be highly accurate at the second order. In Fig. 2, the relative error is about 10-6 and does not drop below that level, which may be the limit of accuracy.

Fig.3 Relative error at z=0.101m on z-axis
Gaussian integral point order dependence

The above discussion assumes that the magnetization of the elements is accurately obtained. Usually, however, a finite element method analysis is first performed to obtain the magnetization of the magnetic material, and then the magnetic field is calculated. Therefore, the accuracy of the magnetization obtained by the finite element method analysis is related to the accuracy of the magnetic field.
The results of solving the problem in Fig. 1 using the finite element method are shown below. To minimize the influence of boundary conditions, a third-order infinite element was used. (However, the use of infinite elements results in extremely slow convergence of the ICCG method and increases the computation time.) Fig. 4 shows the errors in the element center and nodal values of the magnetic field obtained from the finite element analysis. The horizontal axis is 0.2 m in the z-axis direction from the center of the cube; values below 0.1 m represent the magnetic field inside the magnetic body. In the current case, the magnetic field is calculated with an error of 0.3% or less.

Fig.4 Accuracy of magnetic field analysis by finite element analysis

In practice, the accuracy of the magnetization integral depends on both the error in the finite element analysis and the error in the magnetization integral. The accuracy of the finite element analysis can be improved by reducing the element size, and the accuracy of the magnetization integral can be improved by increasing the integration order. In most cases, element center values, nodal values, and interpolated values obtained only by finite element analysis without the addition of magnetization integration errors are considered to be highly accurate. When obtaining the magnetic field by magnetization integration, it is desirable to evaluate its validity by comparing it with the magnetic field obtained by finite element analysis, especially at evaluation points where magnetic materials are in the vicinity. Here, we limited ourselves to the case of a cube with a constant element size.　In the case of elements of other shapes, such as tetrahedrons, or when the element shape is distorted, the trends described here should not change, but care should be taken because errors can be significant.

How to use

The number of Gaussian integration points in a finite element analysis is specified in "Handbook 6. Gaussian Integration Points". Usually, this integration point is also used in the magnetization integration.

* POINTS_IN_1D * POINT_IN_TRIANGLE * MAT_POINTS * 3 7 0

However, if INTEG_OPT=1 in "11.4. Magnetic Field in the Air Region by Magnetization and Current Integration", the number of integration points is set to 1 for the magnetization integration; if INTEG_OPT=1, the calculation accuracy will deteriorate. Therefore, use this function when the evaluation point is far from the magnetic element (at least the element size) and the calculation time is too long. If only post-processing is performed, the order of the magnetization integral can also be changed since the "6. Gaussian Integration Points" specification applies only to post-processing.

* XSYMMETRY * YSYMMETRY * ZSYMMETRY * ROTATION * 0 0 0 0 * NO_POINTS * NO_MAT_IDS * NO_COIL_SERIES * INTEG_OPT * MESH_INPUT * 40 2 0 0 0 * XP(m) * YP(m) * ZP(m) * 0.05248201 0.00137429 0.0575 ・・・・