Summary

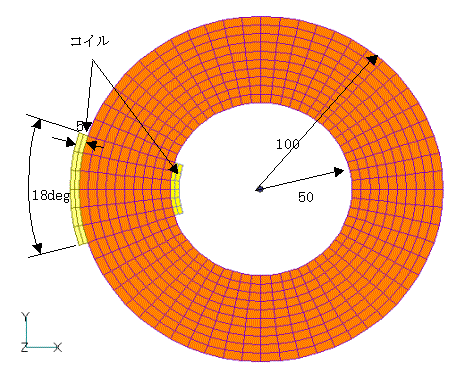
In most cases, the magnetic properties of an magnetic steel sheet will differ in the rolling direction (easy axis of magnetization) and its perpendicular direction. Even materials that are said to be isotropic have different properties. Currently, detailed measurements of anisotropic properties are being made. Here we show an example of anisotropy analysis using EMSolution on a ring model as shown in Fig. 1.

Explanation

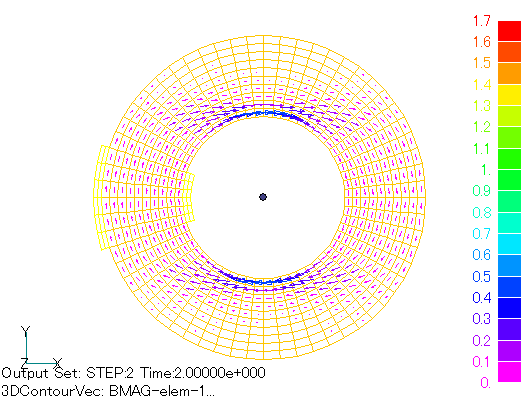
The analysis is two-dimensional. In this model, the magnetic field direction takes all directions, making it suitable for validating anisotropic analysis.Fig.2 shows the overall mesh used in the analysis. Symmetry of the geometry is not used.

Fig.1 Ring model (unit: mm)

Fig.2 Overall analysis mesh

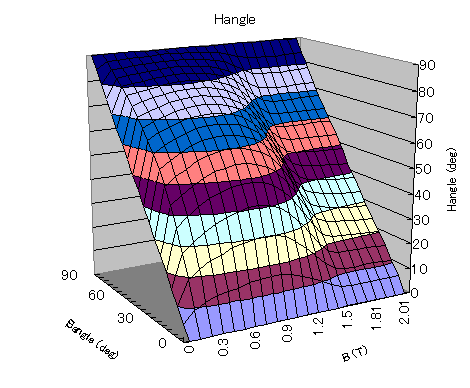
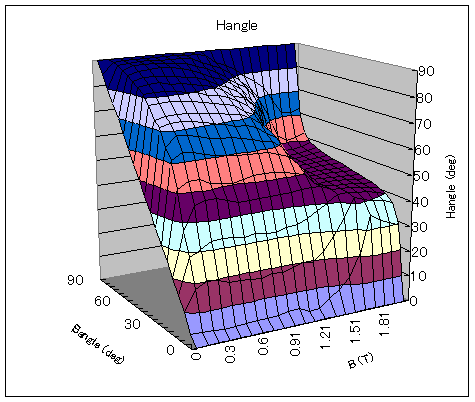
Here, measurement data of 35A300 electromagnetic steel sheet provided by Okayama University are shown in Figs. 3, 4, and 5.
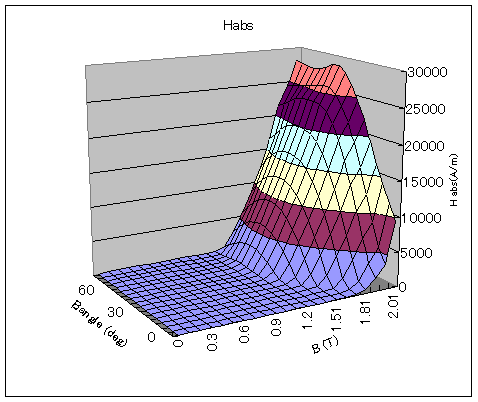
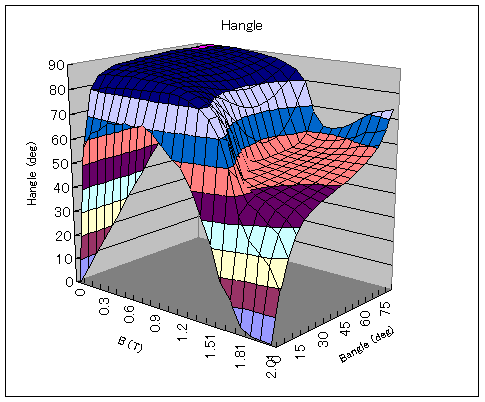
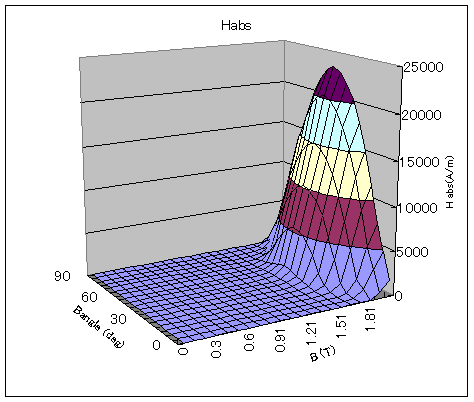
The absolute value and angle of the magnetic field strength $H$ are measured by changing the absolute value and angle of the magnetic flux density $B$ in the measurement. In the angular direction, measurements are taken at 5-degree intervals. The characteristics are close to isotropic, but the absolute value of $H$ differs by a factor of 2 between the rolling direction and the perpendicular direction, and there is also an angle between $B$ and $H$. The data shown here are the measured values as they are, and no smoothing is performed. Although it is possible to smooth the data and use it in the analysis, we will use the data as is. A closer look at the data reveals considerable variation.

Fig.3 Absolute value of H (35A300)

Fig.4 Absolute value of H (35A300, z-scale expanded)

Fig.5 Angle of H (35A300)

In nonlinear convergence calculations, asymmetric matrices appear when using the Newton-Raphson method with data like the above. This makes it impossible to use the ICCG method, which is a symmetric solver. However, it is possible to truncate the asymmetric portions and symmetrize the data for analysis, in which case the ICCG method can be used as before. If the anisotropy is large, the nonlinear iterations will not converge when symmetrized. In this case, an asymmetric matrix solver such as the BiCGStab method should be used. EMSolution offers the option of symmetrization or not symmetrization to choose between the above two methods. 35A300 analysis has fairly good symmetry, so it converges quickly even with symmetrization.
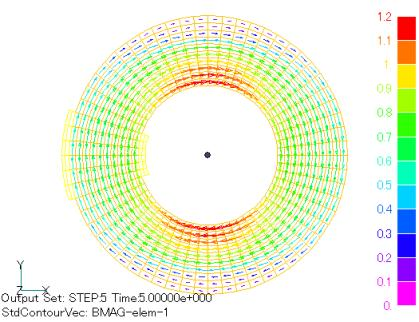
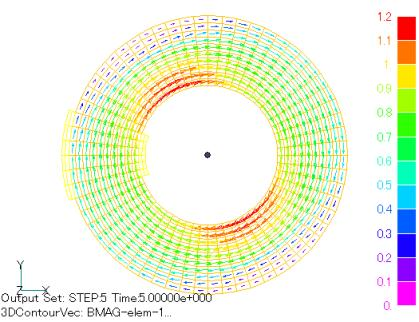
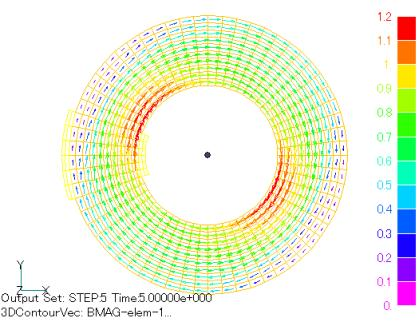
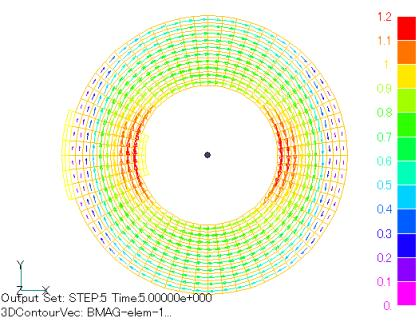
Figures 6 to 9 show the analytical results when the rolling direction is rotated 0, 30, 60, and 90 degrees from the x-axis direction. As expected, the magnetic flux density is rotated by the same angle. More surprising is the concentration of the magnetic field in the area where the magnetic flux flows in the rolling direction (easy magnetization axis). This phenomenon never appears when an isotropic analysis is performed, demonstrating the importance of anisotropic analysis.
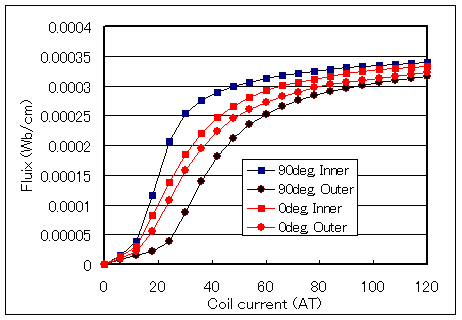
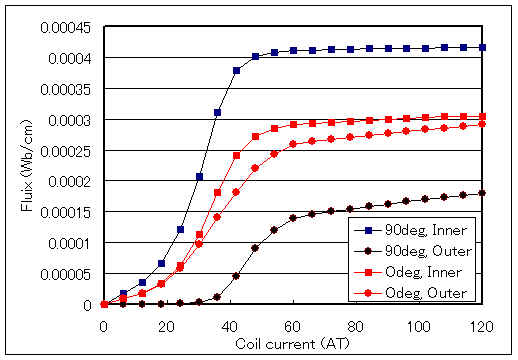
Fig. 10 shows the results of a calculation in which the B-H properties in the rolling direction and orthogonal direction are input and the magnetic properties are independent in both directions. The results are completely different from those shown in Fig. 6, indicating that such an analysis is completely useless. Fig. 10 shows the coil current dependence of the magnetic flux passing through the inner and outer halves at 0 and 90 degrees when the rolling direction is 0 degrees. A large magnetic flux bias is seen at 90 degrees.

Fig.6 Rolling direction 0deg (35A300, 30AT)

Fig.7 Rolling direction 30deg (35A300, 30AT)

Fig.8 Rolling direction 60deg (35A300, 30AT)

Fig.9 Rolling direction 90deg (35A300, 30AT)

Fig.10 Variation of magnetic flux
at 0 and 90 degrees
(0deg in rolling direction, 35A300)

Next, we will discuss the 35G165 material with large unidirectional anisotropy. Figs. 11 and 12 show the measurement data provided by Okayama University. This material is easily magnetized in the 0-degree direction and the magnetic flux is difficult to direct in the 90-degree direction.

Fig.11 Absolute value of H (35G165)

Fig.12 Angle of H (35G165)

The data for the 35G165 material had a lot of bending, etc., and convergence was problematic; the absolute value of H had a large bending at 85 degrees, and the data was smoothed out. The rest of the data were used in the analysis as they were in the original data. When symmetrized, nonlinear convergence was difficult to achieve even with the line-search method, but we were able to obtain a solution with asymmetric analysis.

Fig.13 shows the magnetic flux density distribution when the coil current is varied, and Fig.14 shows the amount of magnetic flux in the inner and outer half at 0° and 90°. It can be seen that the magnetic flux concentration in the inner half at 90 degrees is very large.

Fig.13 Rolling direction 0deg (35G165)

Fig.14 Variation of magnetic flux
at 0 and 90 degrees
(0deg in rolling direction, 35G165)

Finally, we discuss an example of a material with bidirectional anisotropy (called a Cube); Figs. 15 and 16 show the measured data. The material is symmetrical about 45 degrees. The measured data is quite uneven, and the raw data did not show nonlinear convergence, so the data was corrected accordingly. In particular, we corrected Habs to be a monotonically increasing function of $B$ for constant $B$ angle, and $H$ angle to be a monotonically increasing function with respect to $B$ angle for constant $B$. Figs. 15 and 16 show the corrected results, and Fig. 17 shows the flux distribution for this case, which shows a concentration of the magnetic field at 0° and 90°, but not as much as for the unidirectional material.

Fig.15 Absolute value of H (Cube)

Fig.16 Angle of H (Cube)

Fig.17 Analytical results of
bi-directional (Cube)
magnetization characteristics
(rolling direction 0deg, 30AT)

This analysis was performed on an iron core with no air gap, and although it may be an extreme case where a small difference in magnetic resistance causes a large bias in the magnetic flux density distribution, it should give you an idea of the importance of anisotropy analysis. Anisotropy analysis may have a significant impact on the design of electromagnetic equipment. In EMSolution, anisotropy analysis is available in r9.6 or later. It can be used in the same way as earlier nonlinear calculations. It can also be used in transient analysis and sliding motion analysis.

How to use

Specify in NO_2D_B_H the number of nonlinear two-dimensional anisotropic magnetic properties to be defined.

* NO_CURVES * NO_T_DEPEND_CURVES * NO_2D_B_H * 0 0 1

Then enter the number of anisotropic data as specified in NO_2D_B_H.

* BH_2D_ID * NO_B_DATA * NO_ANGLE_DATA * TYPE * 1 22 19 1 * B(T) * H_ABS(0deg)(A/m) *・・・* H_ABS(90deg) * 0 0 ・・・ 0.1 21.769 21.317 21.723 22.658 23.723 24.936 ・・・ 0.201 27.247 27.604 28.603 30.051 31.84 33.639 ・・・ (Omitted below.)

For details, please refer to the sample data and the Handbook.

Download

・ input.35A300
・ input.35G165
・ input.cube
・ pre_geom2D.neu