Summary

Starting with EMSolution ver. 8.6, pyramid (tetragonal pyramid, pentahedron) elements have been added, eliminating the restriction of elements tangent to the axis at a single point. A simple example calculation is shown here. Problems for axisymmetric elements are also described.

Explanation

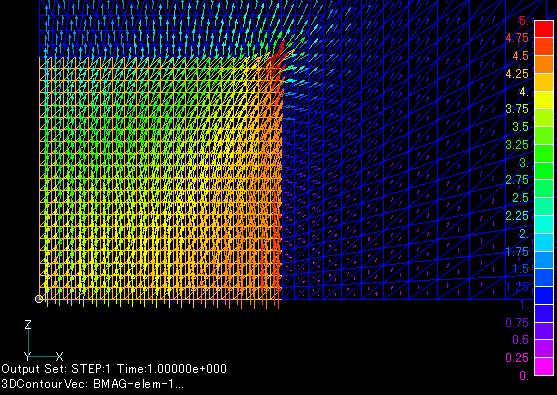
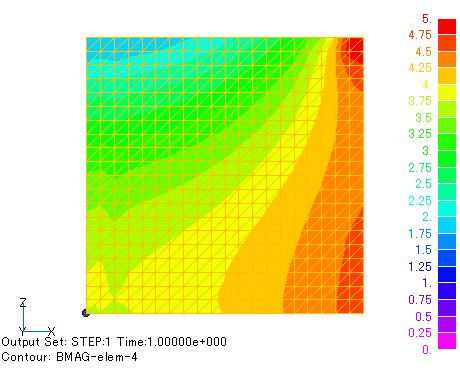
In EMSolution, a two-dimensional mesh is extended to a three-dimensional mesh for two-dimensional analysis. For this reason, in a two-dimensional axisymmetric problem, an element tangent to the axis at one point becomes a square pyramid when extended, and we have requested that such an element not be defined in the past. We have eliminated this restriction by adding pyramid (tetragonal pyramid, pentahedron) elements. Here is a simple example: Fig. 1 and Fig. 2 show the analytical mesh. The domain is divided entirely by triangles, including triangles tangent to the axes at a single point. Conventionally, the points tangent to the axis would have to be rectangles. This model simulates a circular cylinder. Fig. 1 and Fig. 2 show the magnetic flux density distribution and Fig. 3 shows the magnetic flux line distribution.

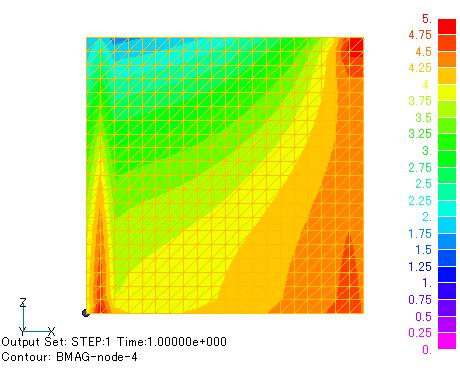
If you look closely at the magnetic field distribution, you can see that the magnetic field is disturbed near the central axis. For example, in Fig. 2, the magnetic field strength oscillates in the radial direction. Fig.4 and Fig.5 show the magnetic field strength distribution. In particular, when the plot is based on nodal data, the strength is higher at a greater distance from the axis. Of course, this is a numerical error, but it is not caused by the pyramid element. The same can be seen with the quadrangle element. Such errors have been known for a long time. This is due to the fact that linear edge elements of warped triangular prisms and hexahedrons cannot represent a uniform magnetic field. In particular, when the magnetic field is obtained by interpolating the shape function, the accuracy of the magnetic field drops at the edges of the element. This is why the result shown in Fig. 5 is obtained. At the center of the element, the accuracy is relatively good and the distribution is quite reasonable when using the element data in Fig. 4. To solve this problem near the center axis, it may be necessary to change the element shape function. For axisymmetric elements, it seems possible to make improvements, which we will consider in the future.
Pyramid elements are not serviced by many common pre-post processors. Therefore, we decided to input and output as an element with the same node number for the top and bottom two points of the triangular prism. However, it is not possible to create such an element in FEMAP, for example. For this reason, the use of pyramid elements is currently limited. In the future, we believe it will be useful when combining hexahedrons and tetrahedrons, and we hope to improve it for everyone’s use in the future.

Fig.1 Analysis mesh and magnetic field distribution

Fig.2 Analysis mesh and magnetic field distribution (enlarged)

Fig.3 Magnetic flux line distribution

Fig.4 Magnetic flux density intensity distribution (Element data)

Fig.5 Magnetic Flux Density Intensity Distribution (Nodal data)

Download

Analysis model　　Sample data DL
・ input
・ pre_geom2D.neu