One of the unique features of EMSolution is the diversity of magnetic field and current sources, as described in EMSolution Basics 4.5. In particular, SDEFCOIL and SUFCUR are distinctive.

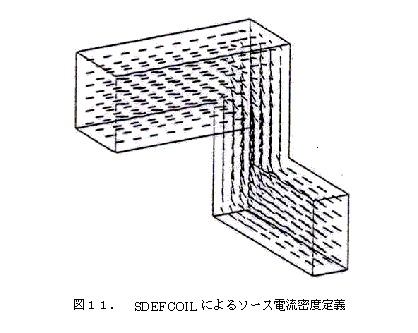
SDEFCOIL[8]. The current distribution is given geometrically rather than by solving for the steady-state current. In the method of solving for the steady-state current, the current concentrates on the inner side of the coil, but in SDEFCOIL, the current flows almost uniformly (Figure 11). Current conservation is strictly established. Technically, two scalar potentials are used, and the current density is expressed as $J=\nabla \phi \times \nabla \psi$

SUFCUR is applied to coils with bulk conductors for which the current distribution is not known a priori. Basically, an electric scalar potential is given at both ends of the conductor and the coil region is solved as an eddy current problem.^[9]

Special elements include gap elements that handle gaps in narrow magnetic materials and insulating surfaces in conductors, thin conductor elements that handle thin conductors, and two-dimensional elements such as the surface impedance element ^[3] that handles steady-state eddy currents with small skin thickness. All of these have their limitations of application, but when used appropriately, they can improve the efficiency of the analysis. If these elements are divided by three-dimensional elements, they require very flat elements, which can seriously degrade the con-vergence of the ICCG method.

In the finite element method, there are difficulties in open domain problems. Usually, a large enough area is taken in the finite element domain to minimize the influence of the boundary. EMSolution provides boundary conditions $B_n$ = 0 and $H_t$ = 0, so that both results can be used to determine how much influence the boundary has on the problem. Infinite boundary elements are also available ^[31]. How-ever, it was only practical for axisymmetric 2D problems, but re-cently a method has been proposed and implemented that is fully applicable to 3D problems.

When solving coupled with external circuit systems and motions, the circuit and motion equations must be coupled with the electromagnetic field equations. In EMSolution, the electromagnetic field equations are coupled to the circuit and motion equations as a single overall matrix. The electromagnetic forces and positions are exchanged with the equations of motion and iteratively calculated. Basically, Crank-Nicolson's theta method is used to discretize the time direction, but it is quite difficult to set the appropriate value of theta in each system of equations, and this may be an important issue. The time constants and other properties of each system are different, and especially in the case of strong nonlinearities, it is questionable whether the $\theta$ method is sufficient. ^[12]