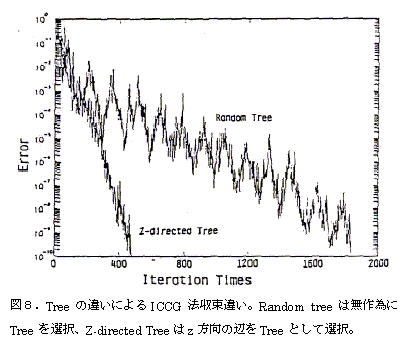
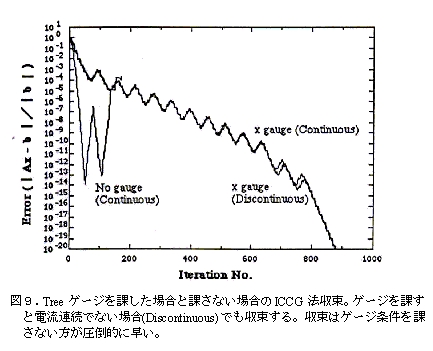
First, the ICCG method can solve indefinite equations that are unique to the edge element method. At the beginning of its development, we thought it was impossible to solve indefinite equations, so we imposed a gauge by tree structure to eliminate indefiniteness. However, although the equations were solvable, convergence was extremely slow. When the gauge condition was removed, an incomplete Cholesky decomposition resulted in a zero division. After some unavoidable investigation, we found that the convergence was a little better depending on how the tree gauge was set, but the convergence was still very slow (Figure 8). However, at Okayama University, they solved the problem at high speed without any gauge condition. After consulting with Mr. Fujiwara of Okayama University (at that time, now Doshisha University),　I noticed that the diagonal component of the matrix was multiplied by a number slightly larger than 1 (I think it was 1.02, which is called the acceleration factor). When I tried this, to my surprise, it was able to solve the problem (Fig. 9). Prof. Fujiwara then studied the acceleration factor in detail and came up with a method to find its optimal value.^[27]

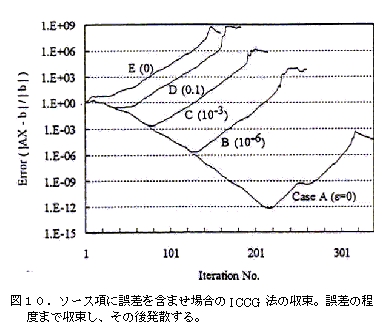
The ICCG method can solve indeterminate equations, but if a current that does not satisfy current continuity is included in the source term of the right-hand side, the equation will have no solution （inconsistent equation）. Even if the equation is not intentionally made indeterminate, numerical analysis can lead to truncation errors and other factors that make an indeterminate equation more or less inconsistent. If this is solved by the direct method, a completely wrong answer will be obtained. However, when solved by the ICCG method, even such equations converge to some extent and then diverge. So, if you take the solution at its most convergent point, you will get something quite accurate.^[8] In addition, the convergence apparently goes to the extent of the errors contained in the equations (Figure 10). Conversely, the convergence error is an indicator of inconsistency in the equation. Occasionally, if the wrong settings are used in the calculation, the ICCG method may not converge at all, and upon review, it may turn out that it was wrong. In this sense, the ICCG method is a good method to show the inconsistency of the equation and its degree.

In the two-potential method, the source term is obtained by integrating the Biot-Savart law. When the source and the integration region (the boundary between the total potential region and the deformed potential region) are close, the error is inevitably large. There are possible ways to eliminate this inconsistency, but EMSolution does not make any correction. For this reason, when the two-potential method is used, the convergence of the ICCG method goes to some extent, but then diverges. However, as mentioned above, taking the solution at the point of greatest convergence gives a reasonable solution, and the problem is small in practical terms. Later, we developed a method to remove errors not only in the two-potential method but also in the current source on the right-hand side, which almost eliminates errors in the current field source and allows the ICCG method to converge to the extent of mesh errors.

In a similar case, when very flat elements (on the order of $\mu m$ thickness) such as the wiring of a substrate are created with 3D elements, it also happens that the convergence of the ICCG method is very slow and, in some cases, does not converge. In such cases, we have confirmed that convergence is much better, and accuracy is ensured when 2D conductor elements are used. In another case, when flat hexahedral or triangular elements are also created in the air layer because the conductor section is meshed considering the skin thickness, the convergence of the ICCG method is very slow. In the literature^[33] , the convergence improvement methods common to the multigrid and $A$-$\phi$ methods (singular separation method, SDT method) can be used to improve the properties of the matrix for faster solution.

Another example of the ICCG method not converging is when solving an eddy current problem using the $A$ method ($\phi$ = 0 gauge) with a very low frequency. In this case, even if convergence is achieved, the obtained eddy currents do not seem to be reasonable. However, when the $A$-$\phi$ method is used, the convergence is about the same as in the static magnetic field analysis, and the solution is reasonable.