Electromagnetic field analysis software

EMSolution Basics 4-1
$A$-$\phi$ method

EMSolution uses a finite element method with edge elements based on the $A$-$\phi$ method which uses magnetic vector potential $A$ and electric scalar potential $\phi$.^[17]

The $A$-$\phi$ method is a fundamental formulation usually used in magnetic field analysis, along with the $T$-$\Omega$ method, but its characteristics compared to the $T$-$\Omega$ method are as follows:

Easy handling of eddy current multi-connected conductors’ problems

Good convergence in nonlinear problems (apparently)

Easy to extend to high-frequency problems including displacement currents (apparently)

On the other hand, in the $T$-$\Omega$ method, the non-conductive region can be treated with a scalar function $\Omega$, whereas the $A$-$\phi$ method requires the use of a vector function $A$, so

It has a disadvantage of greater freedom of analysis

It is known that the $A$-$\phi$ and $T$-$\Omega$ methods have a dual relationship and that, for example, in a static magnetic field analysis, the inte-grated magnetic energy is sandwiched between the values obtained by both methods. From the viewpoint of error evaluation, analysis by both methods may be considered in the future.

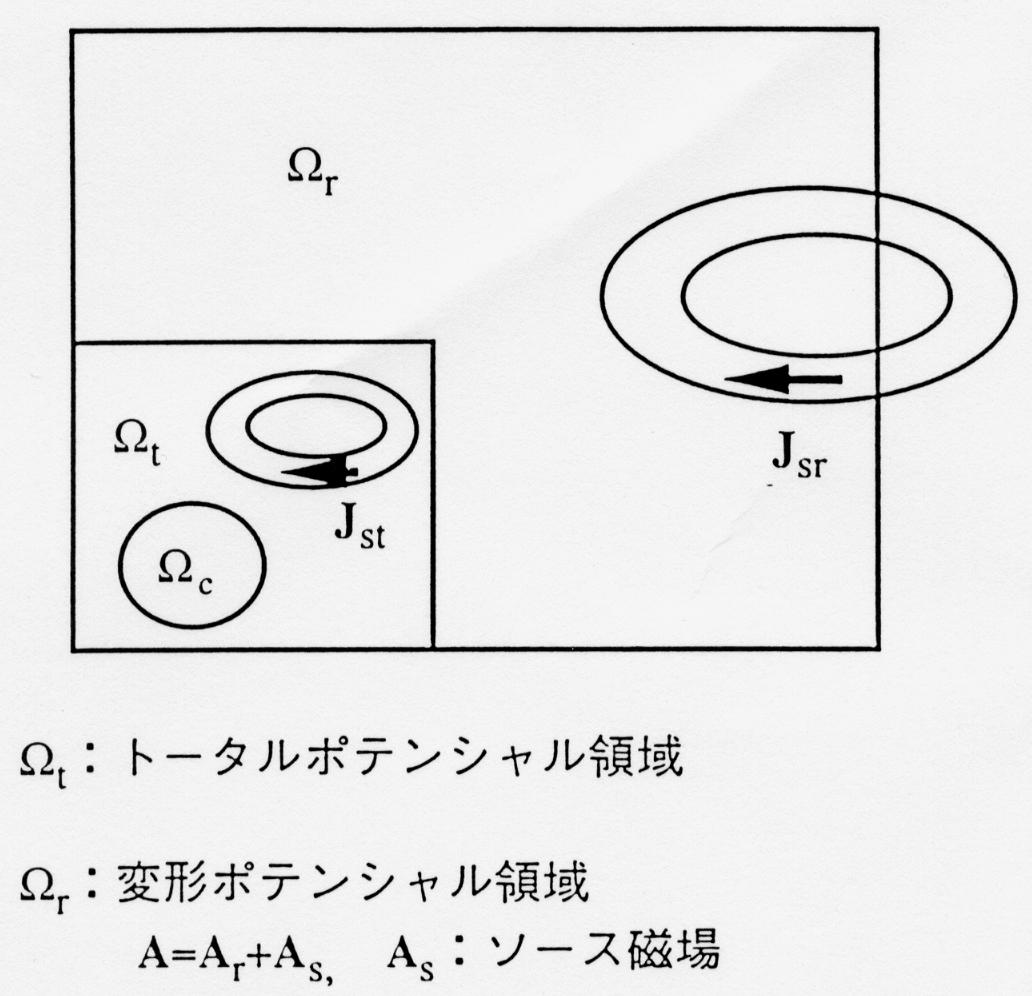
In EMSolution, the $A$-$\phi$ method is basically used, but the magnetic scalar potential $\Omega$ is assumed to be available for the air domain to reduce the number of unknowns. However, the convergence of the ICCG method is quite poor, probably due to the loss of positivity of the system matrix, and it does not help much in reducing the computation time.^[18] It is used only in cases where there is insufficient computer capacity.

Another feature of EMSolution is the use of the reduced magnetic potential $A_r$ for the air domain (2-potential method), where $A_r$ represents the contribution of the magnetic field due to eddy currents and magnetization in the analysis domain, separated from the source magnetic field. The source magnetic field is obtained from the Biot-Savart law.

The advantage of using Ar is that

Source currents can be represented independently of the analysis mesh

The magnetic field due to the source current is not included, so there is no need to make the mesh so fine near the source current.

Source current can be defined outside the analysis area

Source currents can move freely within the analysis do-main, facilitating analysis in the presence of moving con-ductors.^[10]

The two-potential method is often said to take a large amount of computation time to calculate the source magnetic field. This method requires integration of the source magnetic vector potential on the edges and the magnetic field strength ($H$) on the plane at the boundary between the total potential region (where $A$ is the variable) and the reduced potential region (where $A_r$ is the variable). These need only be calculated once and are not such a large burden in EMSolution, except when the source is displaced. There are various analytical integrals for integrating the Biot-Savart law, and you will still need to use them.^[19]