概要

扁平な四面体要素を使用しますと、特に渦電流密度分布に異常が出ることがあります。

解説

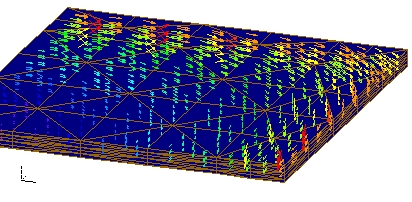
例えば、Fig.2の様な薄板導体に磁場を加えた場合の渦電流は、図のようになります。四面体の分割はFig.1の様に直方体を5つの四面体に分割していて作成しています（分割A）。定常交流解析を行い、周波数を低くしておりますので、渦電流は厚さ方向にほぼ一様になる場合です。一部の要素（直方体分割の中心の要素）で分布がおかしくなっています。

以上の結果は、同じ体積の四面体で直方体を6個の四面体でFig.3の様に分割（分割Ｂ）しても同じように現れます(Fig.4)。この原因は、要素が扁平になり、誤差が大きくなったことに寄ります。
これを解決する一つの方法は、より高次の要素を使用することです。
EMSolutionでは辺一次節点二次の要素(Fig.5、二次要素と呼びます)を導入しました。この要素を導体部に使用しますと、分割Aでも妥当な結果が出ます(Fig.6)。この要素では、節点形状関数を使用しますので、解析は$A-Φ$法で行う必要があります。 もう一つは、Fig.7の様な分割（分割Ｃ）を行うことです。この場合は、一次要素でも妥当な分布となります。分割Ｂと分割Ｃには大きな違いは無い様に見えますが、分割Ｃでは、各要素が直交する三向の辺をもっています。このような要素は誤差が少ないと言われています。ただ、直方体を機械的にこのように分割することは出来ますが、一般のメッシュでは難しいかと考えております。渦電流に表皮効果があるような場合には扁平な要素を使わざるを得ず、メッシュジェネレータにこのようなメッシュが作成できることが望まれます。

Fig.1 一次四面体要素とブロックの四面体分割A

Fig.2 分割Aによる渦電流密度分布の解析結果

Fig.3 一次四面体要素とブロックの四面体分割B

Fig.4 分割Bによる渦電流密度分布の解析結果

Fig.5 二次四面体要素とブロックの四面体分割A

Fig.6 二次要素分割Aによる渦電流密度分布の解析結果

Fig.7 二次四面体要素とブロックの四面体分割C

Fig.8 二次要素分割Cによる渦電流密度の解析結果