概要

EMSolutionでは、電磁力計算は節点力法を用いています（参考文献[1,2])。節点力法は、Maxwellの応力テンソルに、仮想変位を表現する節点形状関数の勾配をかけて積分し、節点にかかる力を出しています。Maxwell応力テンソルは、空気や線形磁性材については明らかなのですが、非線形磁性材に対しては諸説あります。

解説

EMSolutionでは、Maxwellテンソルの表現式として、

$$T_{ij} = H_{i}B_{j}-\delta_{ij} \int_{0}^{H}B \cdot dH$$

を採用しています。磁石等テンソルが対称にならない場合は対称化して使用しております。 ただ、この式はヒシテリスのない非線形材料には使えますが、ヒシテリスや非等方性材料の場合には、疑問があります。 上の積分はいわゆる磁場のco-energy（energyに対して）です。 磁石に対しましては、現状、上の積分を$\frac {B・H}{2}$に置き換えています。 文献[3]では、全ての場合において$\frac {B・H}{2}$で表現されています。 磁性体内では、機械応力場との結合があり、電磁応力と機械応力の分離が難しいのかもしれません。 電磁応力としてどのような表現式を用いれば良いかは今後の課題であると考えています。 一般的に、空気を始め一様な透磁率の物体では、その表面にしか電磁力が現れません。 また、剛体に働く全体の電磁力やトルクは、Maxwell応力テンソルを磁性体内でどのように仮定しても同じになります。 0としてもかまいません。 これは、物体を変形させずに移動した場合には、物体内のエネルギーの変化が無く、電磁力やトルクは物体の周りの磁場分布のみによって決まるためです。 いわゆるMaxwell応力法として知られる、物体の周りの空気領域の表面のMaxwell応力を積分することにより力やトルクを求める方法はこの性質を使っています。 節点力法の場合もこの事情は全く同じです。
さて、例としてFig.1の様なモデルを考えます。 解析は並進二次元計算です。 1Tに磁化された磁石が、磁性板$（m_r=1000）$の上にあるとします。境界条件をFig.1の様にしますと、磁石が極性を交互にして並んでいる場合が模擬できます。 磁性板は上方に引かれるはずです。 磁束分布はFig.2の様になります。 磁性板の下にはほとんど磁場は漏れていません。 磁性板中の磁束分布はFig.3の様になります。 矢印は左方に向かっていて、厚さ方向にはほぼ一様です。 線形材料としたため、磁場は10T以上になっており、実際は飽和が起こりこんなことはあり得ませんが、概念的な話としてご了解下さい。

Fig.1　解析モデル

Fig.2　磁束分布

Fig.3　磁性板内の磁束密度分布

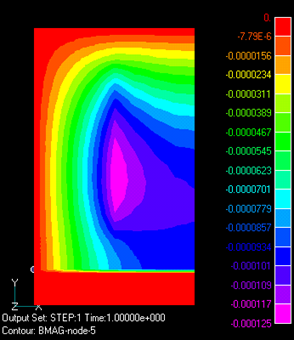
節点力法で求めた、磁性板に働く力をFig.4、5に示します。節点力を要素に働く力に換算しています。Fig.4では、はじめに示した表現式として、磁性体内のMaxwell応力を用いています。Fig.5においては、磁性体内からの電磁応力が無いとしています。トータルの上方向の力は全く同じですが、分布は大きく変わってきます。Fig.4で目立つのは、図で右側の上下の面に働く逆方向の力です。これは、磁性体内の面に沿う磁場が強いために、その拡張力が働くためです。Fig.5では、その力は消え、上面を上方向に引く力となっています。Fig.5の方が直感的には合理的に見えます。

Fig.4　磁性材内のMaxwell応力を考慮した場合

Fig.5　磁性材内のMaxwell応力を無視した場合

参考文献

[1]A. Kameari, “Local force calculation in 3D FEM with edge elements”,
　International Journal of Applied Electromagnetics in Materials 3, 1993, pp.231-240.
[2] 亀有、”節点力法による電磁力解析”、電気学会、
　静止器・回転機合同研究会資料、SA-93-11, RM-93-49, 1993.
[3]今井功、”電磁気を考える”、サイエンス社、1992.