概要

EMSolutionでは磁性体を含む非線形問題において“プレイモデルによるヒステリシス解析”が可能ですが，このたび，ヒステリシスを含まない初磁化特性を用いた従来の磁場解析を行い，ポスト処理でプレイモデルを用いたヒステリシス損の計算機能を追加しましたので説明します。

解説

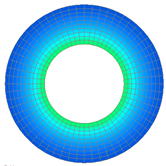
　まず“プレイモデルによるヒステリシス解析”の説明に使用したモデルを使って，初磁化特性で磁場解析を行います。使用した磁化特性をFig.1に示します。 解析結果をFig.2，Fig.3に示します。参考用にヒステリシス解析を行ったときの結果も合わせて示します。

Fig.1　磁化特性

2.5s

5.0s

7.5s

10.0s

(a)　初磁化特性による従来解析

2.5s

5.0s

7.5s

10.0s

(b)　ヒステリシス解析

Fig.2　磁束密度分布

(a)　初磁化特性による従来解析

(b)　ヒステリシス解析

Fig.3　電流と磁束量の時間的な変化

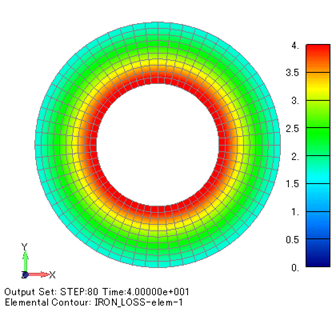
初磁化特性による解析データを使用し，ポスト処理でプレイモデル計算を行い，ヒステリシス損を計算することができます。 Fig.4(a) にヒステリシス損分布を示します。 それぞれの算出法の結果を径方向の分布値としてグラフ化したものを Fig.5 に示します。 Hys-Loss3 ， Norm-Loss3 はそれぞれヒステリシス解析と従来解析においてプレイモデル計算によってヒステリシス損を求めたとき （ 鉄損出力オプション IRON_LOSS(11) = 3 ）の分布です。 Hys-Loss2 ， Norm-Loss2 は，ヒステリシス損係数 （ メーカカタログからの導出値 ） からヒステリシス損を求めた場合 （ 鉄損出力オプション IRON_LOSS(11) = 2 ） の分布です。 ヒステリシス解析を行った結果とポスト処理でプレイモデル計算を行った結果はほとんど同じ結果になります。 Fig.6 に最も内側の要素の周方向の磁束密度 （B_t ） 変化をヒステリシス解析と従来解析それぞれについて示します。 磁束密度の変化は異なりますが，振幅はほぼ同じです。 本モデルにおける磁場変化は交番磁界ですので，プレイモデルの動作を BH 空間で見ると Fig.7 のように同じ履歴になり，ヒステリシス損はほぼ同じになっています。

(a)　従来解析+後処理プレイモデル

(b)　ヒステリシス解析

Fig.4　ヒステリシス損分布　単位[$W/m^3$]

Fig.5　ヒステリシス損分布比較

(a)　評価点

Hys-Bt：ヒステリシス解析時のBt、Norm-Bt：従来解析時のBt
(b)　評価点における磁束密度

Fig.6　磁束密度の時間変化

(a)　従来解析+後処理プレイモデル

(b)　ヒステリシス解析

Fig.7　ヒステリシス損分布　単位[$W/m^3$]

Fig.8に直流偏磁した電流印加をしたときの磁束量の変化を示します。 Fig.9に磁束密度分布の変化を示します。この場合，磁束量は従来解析とヒステリシス解析で異なった振幅で変化する計算結果となっています。Fig.10に従来解析の計算結果を使ってポスト処理でプレイモデル計算を行い，ヒステリシス損を求めたときと，ヒステリシス解析でヒステリシス損を求めたときのそれぞれのヒステリシス損分布を示します。 従来解析の結果は磁場振幅が大きい分高いヒステリシス損になっています。 最も内側の要素の周方向の磁束密度変化をFig.11に， BH の振る舞いをFig.12に示します。 このFig.12からわかるように，初磁化曲線では $H = H_{max}$ から0に変化する際， $B$ は $B_{max}$ から $0$ に戻りますが，ヒステリシス解析では， $H = H_{max}$ から$0$に変化しても $B = 0$ にならず，ヒステリシス磁化特性の $H = 0$ と $H_{max}$ の間で磁場が変化します。 従来解析の結果をプレイモデルのポスト処理を行った場合は， $B$ が $B_{max}$ から$0$まで変化する動作になるため，ヒステリシス磁化特性において $H_{min}$ は$0$よりも負側の値になります。 Fig.7のような直流偏磁がない場合は， $H = H_{max}$ に対応する $B$ の値 （ $B_{max}$ ）とそこから $H = -H_{max}$ に変化したときの $B$ の値（ $-B_{max}$ ）が初磁化特性とヒステリシス磁化特性で同じになるので，上述のようにヒステリシス損の計算値もほぼ同じ値に計算されるということになります。
このように，磁束密度の振幅がほぼ同じであれば，従来解析の結果を用いてポスト処理でプレイモデル計算することにより，同様のヒステリシス損を得ることができますが，そうでない場合は，誤差が大きくなることもあります。 本モデルではほとんど発生しない回転磁界を生じるような場合も，ヒステリシス損計算値は異なってくるものと思われます。 また上述のリング試料の磁束量の時間変化をヒステリシスの効果を考慮した形で計算する必要があるときは，ヒステリシス解析を行う必要があります。 たとえば，上述の同じリング試料でも電圧駆動の場合は，ヒステリシス解析を行った方がより実際に近い結果を得られるものと思われます。

(a)　初磁化特性による従来解析

(b)　ヒステリシス解析

Fig.8　電流と磁束量の時間的な変化

2.5s

5.0s

7.5s

10.0s

12.5s

15.0s

17.5s

20.0s

( a )　初磁化特性による従来解析

2.5s

5.0s

7.5s

10.0s

12.5s

15.0s

17.5s

20.0s

( b )　ヒステリシス解析

Fig.9　磁束密度分布

(a)　従来解析+後処理プレイモデル

(b)　ヒステリシス解析

Fig.10　ヒステリシス損分布　単位 [$ W/m^3 $]

Hys-Bt：ヒステリシス解析時のBt、Norm-Bt：従来解析時のBt

Fig.11　磁束密度の時間変化

(a)　従来解析および
プレイモデルあと処理

(b)　ヒステリシス解析

Fig.12　 H-B 動作

以上の解析条件と結果をまとめたものを Table1 に示します。

Table1　解析条件とヒステリシス損

従来解析 : 初磁化特性による従来の磁場解析
ヒス解析 : プレイモデルによるヒステリシス解析
ヒス損A : ヒステリシス損係数を用いたポスト処理
ヒス損B : プレイモデル計算