概要

静止器や同期電動機に対して，TP-EEC法を適用すると，高速に定常解を得ることができることを“時間周期問題の定常解への高速収束”において示しました。さらにその簡易版として，簡易EEC法を誘導機の解析に適用して定常まで高速に定常付近まで収束できることを“簡易版時間周期法による誘導電動機の定常解析”において示しました。ここでは，簡易EEC法の拡張版として，多相交流の場合の高速化手法をEMSolutionに導入しましたので，報告します。

解説

多相交流とは，二相以上の交流に適用できる方法で，基本的な考え方は簡易EEC法によります。簡易EEC法とは，半周期性に対して補正を行うもので，時間ステップ解析において，ある時点の方程式の解$x_0$と半周期後の$x_n$を使用して$x_0=-x_n$の関係を用いて補正を行うものです。

例として三相交流の場合で説明すると，三相交流での$x_0$と$x_n$の関係式は，以下のように書けます。

$${ x_{0}= \begin{Bmatrix} x_{0}^{1} \\ x_{0}^{2} \\ x_{0}^{3} \\ \end{Bmatrix} = \begin{Bmatrix} x_{n}^{2} \\ x_{n}^{3} \\ -x_{n}^{1} \\ \end{Bmatrix} = \begin{bmatrix} O & I & O \\ O & O & I \\ -I & O & O \\ \end{bmatrix} \begin{Bmatrix} x_{n}^{1} \\ x_{n}^{2} \\ x_{n}^{3} \\ \end{Bmatrix} =Gx_{n} }$$

ここで，上添え字は相順を表します。簡易EEC法と同じ考えのもと，補正方程式は以下のように表せます。

$${ \begin{Bmatrix} p^{1} \\ p^{2} \\ p^{3} \\ \end{Bmatrix} = -\frac{1}{2} \begin{Bmatrix} (x_{0}^{1}+x_{0}^{2}+x_{0}^{3})+(x_{n}^{1}-x_{n}^{2}-x_{n}^{3}) \\ (-x_{0}^{1}+x_{0}^{2}+x_{0}^{3})+(x_{n}^{1}-x_{n}^{2}-x_{n}^{3}) \\ (-x_{0}^{1}-x_{0}^{2}+x_{0}^{3})+(x_{n}^{1}+x_{n}^{2}+x_{n}^{3}) \\ \end{Bmatrix} }$$

得られた補正量 $p$ より，$x_n← x_n+ p$ として補正を行います。これは半周期性に対して成り立つもので，半周期を1/3したステップ毎で補正される，つまり半周期で３回補正できることになります。補正される三相交流は，Fig.1のように半周期性を持ちます。 これは，60deg.ずつ（=180/3）の位相差を持つ３相で，一般の三相交流は２番目の相を反転させたもの（-２）として表されます。回転機のステータコイルに適用する場合，U+，W-，V+が60deg.ずつ位相差を持っていることから，適用が可能となります。 ３相や５相のように，奇数相（2m +1）は，補正する相数と実際の相数が一致しますが，偶数相である２相や６相ではやや異なり，2m×2相での半周期補正となりますが，補正方程式は2m 相で同様に導くことができ，補正可能となります。
例えばFig.2に示すように，２相を半周期性で補正したい場合，90deg.ずれた４相交流を補正していることになります。補正は半周期の1/2毎で行えます。
多相交流簡易EEC法でも，簡易EEC法同様，補正のために方程式を解く必要が無く，簡便でかつ相数分補正回数を増やすことができます。

Fig.1 三相交流

Fig.2 4相交流

１. 検証モデル

まず簡単な場合として，Fig.3に示す多相交流モデルについて示します。コアにコイルがはめ込まれ，ギャップを介し導体が配置されています。コアは線形材料とし，比透磁率1000，導体には適当な導電率を与えています。X方向は反周期境界条件とし，導体は静止しているものとして解析します。この時，多相交流簡易EEC法の補正対象はコイル部とします。時間差分は，TP-EEC法や簡易EEC法同様，THETA=１とした方が安定するようです。
ここで制限として，補正される導体のメッシュは，相間で節点，要素数が同じ，形状（座標）は周期性を持っている必要があります。

Fig.3 検証モデル（5相モデル）

解析は，一番左の相を基準相とし，右側に一層ずつ増やしていき，２～８相まで計算を行いました。先にも述べたように，補間を２～８相で行うため，2m 相は実質４,８,１６相となります。 ２，３，５，８相での解析結果であるコイル電流をFig.4に示します。相数が多くなればなるほど，補正回数が増えるため，早い段階で補正されていることがわかります。全ての相で，多相交流簡易EEC法（P-EEC：Polyphase EEC）で補正することができています。これより，多相交流簡易EEC法が非常に有効であることがご理解頂けると思います。

(a) 2相

(b) 3相

(c) 5相

(d) 8相

Fig.4　検証モデルの多相交流簡易EEC法によるコイル電流

2.同期電動機モデル

同期電動機のモデルとして，“時間周期問題の定常解への高速収束”で使用したIPM 同期モータモデルに適用してみます。ただし，モデルはFig.5に示す，“半周期性を利用した鉄損算出”で使用した二次元モデルで，正弦波電圧源解析とします。磁場ソースとなる導体を補正対象とするため，導体に接続される電気回路の電流値や鉄心等は補正されませんが，先の例題のような補正効果が期待できます。本IPM 同期モータの場合でも，60deg.で半周期性ですので，ステータコイルは20deg.=60/3の周期性を持っているため，座標は20deg.毎にずれ，節点，要素数は全く同じとしています。
Fig.6にステータコイルにTP-EEC法（EEC），簡易EEC法（S-EEC：Simplified EEC），多相交流簡易EEC法を適用した結果と，補正を行わない計算（Conventional）を比較して示します。この時，ステータコイルの電源周波数は50Hz（0.02sec=40steps）としています。同じ半周期毎に補正できるTP-EEC法の方が簡易EEC法よりも早く定常に達しており，さらに半周期の1/3毎に補正できる多相交流簡易EEC法の方が素早く定常に達しています。これより，多相交流簡易EEC法の補正効果が高いことがわかります。ただし，このモデルはステータコイルの他に（渦）電流が流れる箇所が無い二次元解析のため，ステータコイルの時定数により補正効果が顕著に出ることから，効果が大きいとも考えられます。

Fig.5 IPM同期モータ

Fig.6 IPMモータ　ステーたコイル電流

3.誘導電動機モデル

Fig.7に示す，“かご型誘導電動機の一極分でのモデル化”で使用した誘導機の一極分モデルに，多相交流簡易EEC法を適用してみます。なお，補正対象とする導体部分が形状的にも半周期性を持つ必要があるため，一極分でのモデルを使用しています。すべりs=0.25での正弦波電圧源解析を行います。まずはステータコイルに三相交流簡易EEC法を適用した結果と，ステータに簡易EEC法を補正した結果を比較して示します。この時，ステータの電源周期50Hz（0.02sec=36steps）としています。Fig.8にステータコイル電流波形を，Fig.9にロータバー電流波形を示します。三相交流簡易EEC法では6steps毎と，簡易EEC法の18steps毎に比べ３倍補正能力があるため，素早く定常に達しています。

Fig.8 誘導電動機モデル
電圧源解析時のステータコイル電流

Fig.9 誘導電動機モデル
電圧源解析時のロータバー電流

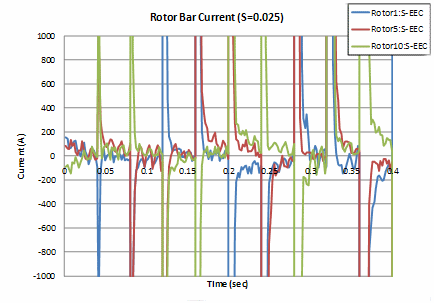
次に，ロータバーに多相交流簡易EEC法を適用することを考えます。一般にロータバーはステータコイルよりも本数が多いため，３相以上の相数での補正が可能で，補正効果が期待されます。今度はステータコイルを電流源解析とし，ロータバーは10本ですので10相補正（実質20相）が可能となりますので，多相交流簡易EEC法を適用してみます。 すべりs=0.25とした場合の結果をFig.10(a)にロータバーの電流波形を，簡易版EEC法により得られたすべり周期２周目の定常状態のものと，補正を行わないものと合わせて示します。すべり周期は12.5Hz（=0.08sec）で，補正は半周期の1/10ステップ毎に行われます。計算初期を見ると，補正回数４回（0.02sec）くらいまでは精度よく補正され，その後は補正の度に発散してしまっています。これは，ロータバー間の電流波形は，たとえ定常に達したとしてもロータバーの相間で同じ波形にはならないため，自相だけでなく他相も使用して補正して相間で同じ波形になることを前提としている多相交流時間周期法では，低次の誤差が大きいステップで補正効果が出て定常に近付きはするものの，その後発散してしまうと思われます。すべり0.025，0.75でも計算してみたところ，すべり0.025では補正した途端に発散していってしまいましたが，すべり0.75ではすべり0.25と同様，最初の数回の補正は可能で，その後発散していく傾向がみられました（Fig.11）。これより，ロータバーに適用する場合，基本波に対するスロット高調波の割合（振幅）が補正に大きく影響し，すべりが小さい場合は基本波が小さいうえにスロット高調波がのるため補正効果は無く，すべりが大きい場合は，スロット高調波に対して基本波が大きくなるので，最初の数回であれば効果があると言えるかと思います。すべり0.25において精度よく補正されている補正回数５回目の0.02secを初期値としてリスタート計算を行ったところ（Fig.10(b)），素早く定常状態になりましたので，誘導機解析においてロータバーに多相交流簡易EEC法を適用する場合は，計算初期の定常までの収束を早めるために使用して頂ければと思います。 なお，ステータコイルの電圧源解析でも，ロータバーに多相交流簡易EEC法を適用することが考えられますが，ステータコイル電流はロータバーの補正効果を受け補正されるため，ステータコイル電流に依存しているロータバーのみを補正しても効果は無いようです。

(a)　計算初期時の定常値との比較

(b)　時刻0.02secからのリスタート

Fig.10　誘導電動機モデル
電流源解析時のロータバ－電流

(a)　すべりS=0.025

(b)　すべりS=0.75

Fig.11　誘導電動機モデル
電流源解析時のロータバー電流（すべり変更）

これより，多相交流簡易EEC法が有効であることを示せたと思います。静止器や同期機で，多大ステップを計算する際には，簡易法ですがTP-EEC法よりも相数倍補正能力のある多相交流簡易EEC法が有効かと思われます。誘導機に適用する場合は，電圧源解析の場合はステータコイルに，電流源解析ですべりがやや大きい場合には，ロータバーに適用して，計算初期の数回補正で定常値まで素早く収束させることができると思われます。ただし，どちらの場合も簡易EEC法同様，半周期ごとにステータとロータバーの位置関係が必ずしも一致しないため，かなり定常解には近くなっていると思いますが厳密には定常解とはなりません。そのため，“周期的に印加される磁場に対する解の収束性”と同様の考え方で，最初は簡易版時間周期法で定常解に近いところまで計算し，それを初期値としてリスタート解析を行って定常解を得る，というようにお使い頂ければと思います。 また多相交流簡易EEC法では，コイルやロータバーをSUFCURとして定義して解析することが可能となります。