OpenMPによる並列計算機能
- TOP >
- 機能別解析例・解析技術(一覧) >
- OpenMPによる並列計算機能
概要
これまでEMSolutionは,大規模・高速化を目指して開発を行ってきました。 近年,マルチCPU,マルチコアマシンが一般的になってきたため,当社でも部分的にですが並列機能を追加しましたのでご紹介します。
なお,並列化は1ノード(1台のWS)で行えるOpenMPによるものであるため,搭載されているコア数以上の並列計算はできません。しかし,台数効果は出やすいため,比較的大規模な三次元解析を行うのに適しています。 今回ご紹介するのは,以下の3つの並列機能についてです。他の部分についても,順次並列化を進めていく予定です。
- ICCG法の並列計算
- B_INTEGの並列計算
- MeshedCOILの並列処理
解説
ICCG法の並列計算
ICCG法は線形対称行列解法で,通常の静磁場,過渡解析解析に使用されるものです。 磁化特性が線形,非線形を問わずに使用できます。 行列が非対称になる二次元磁気異方性等には適用できませんのでご注意ください。 ICCG法の並列化にはBlockICCG法を採用しており,非線形磁化特性計算で使用されるNewton-Raphson法の計算の一部も並列化をしています。
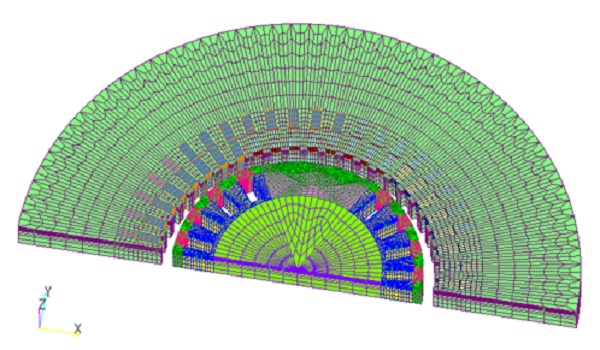
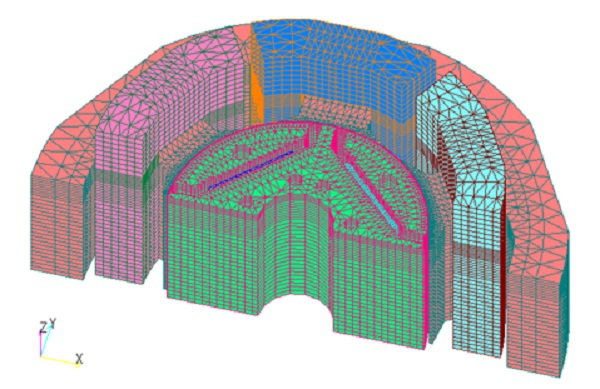
例として,Fig.1に示す発電機モデルと電気学会ベンチマークモデルである集中巻IPMSM(D1モデル)の三次元解析に適用した結果を示します。 解析は非線形過渡磁場解析で,電流源としています。Table 1とFig.2に発電機モデル,Table 2とFig.3に集中巻IPMSMの台数効果を示します。 収束がいい発電機モデルでは2, 4並列とほぼ線形に台数効果があがります。 D1モデルではあまり収束が良くないこともあり,4並列でやや下がっています。 これはBlockICCG法では,BlockIC分解を行うため,並列数が増えると収束が悪くなり,ICCGの反復回数が増加する傾向があるためです。 しかし,シングル(1並列)で計算するよりかは1.9倍高速に計算できています。
このように,BlockICCG法による並列化は,単純に並列数を上げると計算時間を短縮できるため,有用だと言えます。 なお,台数効果は搭載CPUの性能に強く依存するようです。
本例で使用したマシンは,CPU:Intel Xeon E5520(64bit,Nehalem),2.26GHz,4コア。ハイパースレッドは使用しない。 メモリ:12GBで,台数効果が出やすいCPUのようです。
Table1 発電機モデルの台数効果
| 並列数 | 並列時間(s) | ICCG反復回数 | NR反復回数 |
|---|---|---|---|
| 1 | 184.4 (1.00) | 733 (1.00) | 15 (1.00) |
| 2 | 118.3 (1.56) | 763 (1.04) | 15 (1.00) |
| 4 | 85.8 (2.15) | 824 (1.12) | 15 (1.00) |
Table2 集中巻IPMSMモデルの台数効果
| 並列数 | 並列時間(s) | ICCG反復回数 | NR反復回数 |
|---|---|---|---|
| 1 | 391.8 (1.00) | 2946.2 (1.00) | 7.5 (1.00) |
| 2 | 232.6 (1.68) | 2982.1 (1.01) | 7.4 (0.99) |
| 4 | 206.8 (1.89) | 3451.7 (1.17) | 8.9 (1.18) |
B_INTEGの並列計算
"磁化および電流の積分空間磁場(B_INTEG)"にも並列計算機能を追加しました。
これは磁性体,導体以外の空間磁場を,メッシュ形状に依存せず,任意位置での高精度に磁束密度を出力することができます。これは並列計算に非常に適しているため,理想的な台数効果が出ます。
例として,Fig.4に示す,"コイルのみの磁場分布計算"で用いたモデルで台数効果を検証します。 評価点を評価点は0~250mmを各軸方向格子状に①50等分,②100等分し配置しています。台数効果をTable 3に示します。ほぼ理想的に台数効果が得られていることがわかります。 なお,使用マシンはQuad Core Intel Xeon 3.00GHz×2CPU (計8Core)です。本機能はCPUによらず,台数効果が得られるようです。
Table3 台数効果
| B | 100分割 | 50分割 | ||
|---|---|---|---|---|
| スレッド数 | 計算時間(sec) | 台数効果 | 計算時間(sec) | 台数効果 |
| 1 | 24.656 | 1.000 | 3.282 | 1.000 |
| 2 | 12.516 | 1.970 | 1.656 | 1.982 |
| 4 | 6.344 | 3.887 | 0.844 | 3.889 |
| 8 | 3.188 | 7.734 | 0.438 | 7.493 |
| 評価点数 | 1,030,301 | 132,651 | ||
MeshedCOILの並列処理
"6面体要素メッシュによるCOIL(外部電流磁場ソース)の定義(MeshedCOIL)"にも並列処理機能を追加しました。
これは六面体の有限要素メッシュでCOILを定義できる機能で,計算量は六面体要素と積分点に比例します。
この中の"COILのインダクタンスおよび電磁力計算機能(COIL_INDUCTANCE)"や"非線形オプション比較"で紹介されている電流の連続性を保証するREGULARIZATION機能や,磁束密度出力等で並列処理されます。例として,Fig.5に示す発電機モデル(Fig.1とは異なる)の電機子コイルをMeshedCOILでコイルエンドまで含めてモデル化したものに適用できます。ロータの界磁コイルはCOILにてモデル化しています。電機子コイルのMeshedCOILは有限要素メッシュ内のReduced Potential領域が周期境界条件となるため,有限要素メッシュのような対称性が適用できず,全周モデルでモデル化しています。界磁コイルのCOILは周期境界面に触れないCOILの周りのみReduced Potential領域としているため,有限要素領域内のみのモデル化で対応できます。 ロータ,ステータでCOILを使用しているため,"マルチポテンシャル法"を使用しています。
このモデルは電圧源とすると時定数が長いため,TP-EEC法が必須となり,Meshed_COILとICCG法の並列機能が適用できます。
OpenMPによる並列計算機能 限定した機能ではありますが,OpenMPによる並列計算機能は有用なことが示せたと思います。
更なる大規模解析が必須となりつつありますので,是非ご試用いただければと思います。導入前の評価も受け付けておりますので,お気軽に"こちら"から問い合わせください。
この先は会員の方のみご覧いただけます。
機能別解析例
収束特性改善、高速化手法
- INIT OPTIONの効果
- 非線形オプション比較
- 収束条件と解析精度
- 扁平四面体要素の問題点とその解決法
- 節点二次辺一次要素
- 六面体要素と四面体要素の接合
- 扁平・扁長要素の収束性の改善
- 周期的に印加される磁場に対する解の収束性
- 時間周期問題の定常解への高速収束
- 簡易版時間周期法による誘導電動機の定常解析
- 多相交流簡易EEC法による回転機の定常解析
- 時間周期条件を利用したdq軸座標系でのTP-EEC法(dq-TP-EEC法)
- 変形ポテンシャル領域に配置する外部磁場電流ソースのICCG法収束性に対する影響
- OpenMPによる並列計算機能
- 収束条件変更のリスタート解析
- 定常周期性を利用した反復計算時の初期値設定
キーワード
©2020 Science Solutions International Laboratory, Inc.
All Rights reserved.