概要

EMSolutionで電気回路との接続を考慮するためには，NETWORKとCIRCUITによる方法があります。NETWORKは回路図に書かれた回路素子や電源とその接続を入力データとして設定する方法であるため，直観的でわかりやすいと思われます。

解説

一方，CIRCUITは回路の接続を独立な変数だけに整理し，その接続を行列で与えるため，直接解くべき回路方程式を表現するような方法となります。従って，CIRCUITは入力データの作成が難しいこともあり，あまり複雑な計算には向かないと思われます。しかし，NETWORKはオプションモジュールであることもあり，簡単な回路ではCIRCUITだけで済ませたいと思われることもあるかと思います。そこで，ここではよく使用される三相回路を例として，NETWORKとCIRCUITの対応について説明します。

NETWORK

NETWORKは回路図より回路素子やその結線をEMSolutionのinputに記述する方法であり，直観的であるために理解しやすいと思われます。そこで，まず計算するモデルの回路図を示し，CIRCUITとの比較を明確にするため，NETWORKによるデータを作成してみます。

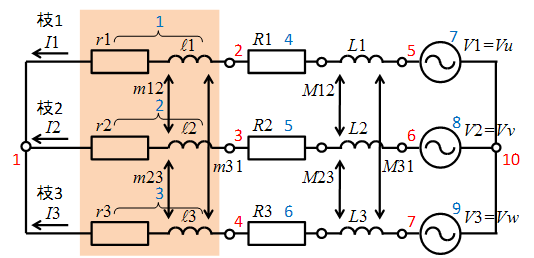
Fig.1に三相回路の回路図を示します。図中の青字は素子番号を，赤字は端子番号を表します．この回路は"かご型誘導電動機の一極分でのモデル化"に接続された回路であり，メッシュやinputファイルなどをダウンロードすることができます。
Fig.1の橙色の部分は，要素分割され有限要素法でコイルとして磁界解析を行う領域です。また，回路の各相に直列な部分を枝と呼び，それぞれの枝を枝1，枝2，枝3とします。以降，素子，電源等の添字は各枝番号に対応します。このメッシュ内のコイルの抵抗（$r_1$，$r_2$，$r_3$）， 自己インダクタンス（$l_1$，$l_2$，$l_3$）， 相互インダクタンス（$m_{12}$，$m_{23}$，$m_{31}$） はEMSolution内部で考慮されるので，ユーザがその値を指定する必要はありません。（コイル抵抗はEMSolutionで計算せずに，外部抵抗の一部として与えることもできます）。

Fig.1 NETWORKにおける三相回路図

次に，回路のメッシュに含まれない外部素子やケーブルなどの外部抵抗 (R1, R2, R3)、外部自己インダクタンス (L1, L2, L3)、外部相互インダクタンス (M12, M23, M31) はNETWORKの抵抗要素 R、インダクタンス要素L、相互インダクタンス要素Mとして設定します。また，定電圧電源は，電圧源要素VPS，定電流電源は電流源要素CPSとして設定します。ここでは定電圧電源VPSとし， V1、V2、V3は大きさが等しく位相が順に120度ずつ遅れたU，V，W相の三相電圧条件を与えます。従って，(1)式が成立します。

$$\begin{array}{r}\begin{array}{l}{\displaystyle V1=V{e}^{j\omega t}}\\ {\displaystyle V2=V{e}^{j(\omega t–2\pi /3)}}\\ {\displaystyle V1+V2+V3=0}\end{array}\} (1)\end{array}$$

Fig.2のようにinputファイル中のNETWORKのデータを設定します。ただし，外部自己・相互インダクタンスは考慮せず，メッシュのコイル抵抗は外部抵抗Rとして全て2.92Ωとしています。ロータバーの導電率を$1.01\times {10}^7$S/mとして与え，SUFCURで定義することで，ロータバーの抵抗はEMSolution内部で計算されます。Fig.2の下2行はロータバーの回路で，三相回路とは直接関係なく，ロータバーの電源は定電流電源CPSとし，その大きさは0とする。このように大きさ0の定電流電源CPSと接続することで，回路が短絡している，つまり電流を保存させることを表します。

Fig.2 NETWORKのinput

Fig.3は定電圧電源に与える時間関数です，その大きさ，位相などの時間的な変化を示します。電圧の大きさは線間電圧100Vを相電圧に変換し，最大値とした V（≒81.649V），周期は0.2s（周波数50Hz），位相はU，V，W相がそれぞれt=0のとき0，-120，-240度です．

Fig.3 NETWORKのinput（時刻部分）

Fig.1の変数と対比すると，(2)式のようになることがわかります。

$$\begin{array}{r}\begin{array}{l}{\displaystyle R_1=R_2=R_3=2.92}\\ {\displaystyle L_1=L_2=L_3=M_{12}=M_{23}=M_{31}=0}\\ {\displaystyle V_1=81.649e^{j\omega t}, V_2=81.649e^{j(\omega t–2\pi /3)}, V_3=81.649e^{j(\omega t–4\pi /3)}}\end{array}\} (2)\end{array}$$

$I_1$、$I_2$、$I_3$は未知変数ですが，三相対称回路であるため次式が成立します。

$${\displaystyle I_1=I_2=I_3=0 (3)}$$

定電源電圧は三相対称として入力データを与えますが，得られた解析結果は，一般的には電流は三相対称になるとは限りません。本解析の例でもある"かご型誘導電動機の一極分でのモデル化"のメッシュ形状は三相に対する対称性はないため，内部インダクタンスは等しくならず， $I_1$，$I_2$，$I_3$ は対称とならないことからもわかります。
線形交流定常解析（AC）を実行します。モデルは誘導機ですので，本来材料非線形性とすべり周波数，スロット高調波の影響が電流波形に現れてきますが，AC解析であるため，材料は線形とした結果が得られます。t=0におけるoutputの回路素子に関する結果はFig.4のようになります。

**************************************************************************** * Step No. 1 Time 0.0000000000e+00 sec * **************************************************************************** *** Network elements ***************************************************** ID No. Current Voltage Flux 1 -3.03495e+00 7.30453e+01 -1.63183e-02 2 2.94163e+00 -3.19766e+01 2.07350e-01 3 9.33242e-02 -4.02936e+01 -1.94012e-01 4 -3.03495e+00 8.86207e+00 5 2.94163e+00 -8.58956e+00 6 9.33242e-02 -2.72507e-01 7 3.03495e+00 8.16490e+01 8 -2.94163e+00 -4.08245e+01 9 -9.33242e-02 -4.08245e+01

Fig.4のID No.はFig.1の青字で示された素子番号に対応しており，1～3はメッシュのコイル，4～6は外部抵抗，7～9は電源であり，それぞれに流れる電流及び電圧位相差を表しています。また，1～3はコイルに鎖交する磁束量も示されています。これは"外部電流磁場ソース（COIL）におけるインダクタンスの取り扱い"でも説明されているように，ターン数あたりのコイル鎖交磁束量となっております。電流や電源の電圧の条件式(1)，(3)をいずれも満足していることがわかります。ここでは示しませんが，t≠0以外の結果も同様に満足しています。

CIRCUIT

CIRCUITはNETWORKのように回路図をそのまま扱わず，独立な閉ループを設定する方法です。よく知られているように，独立な閉ループの数はグラフ理論における補木（co-tree）の数となります。Fig.1の回路における独立な閉ループ数は2であるので，Fig.5に示すような閉ループA、Bを定義し，それぞれのループに流れる電流を閉路電流$I_A$、$I_B$とします。すると，NETWORKで定義した枝電流$I_1$、$I_2$、$I_3$と閉路電流$I_A$、$I_B$は次のような行列式の関係が成立します。

$$\left\{\begin{array}{c}{I}_1\\ I_2\\ I_3\end{array}\right\}=\left[\begin{array}{cc}1& 0\\ 0& 1\\ -1& -1\end{array}\right]\left\{\begin{array}{c}{I}_A\\ I_B\end{array}\right\} (4)$$

同様に，NETWORKで定義した各枝の電源の電圧はV1、V2、V3と閉ループの電源の電圧$V_A$、$V_B$は次のような行列式の関係が成立します。

$$\left\{\begin{array}{c}{V}_A\\ V_B\end{array}\right\}=\left[\begin{array}{ccc}1& 0& -1\\ 0& 1& -1\end{array}\right]\left\{\begin{array}{c}{V}_A\\ V_B\\ V_C\end{array}\right\} (5)$$

(5)式で表される枝と閉ループの関係を表す行列を閉路行列，またはタイセット行列といいます。(4)，(5)式からわかるように，枝と閉ループの電流，電圧の関係を表す行列は転置行列となります。

Fig.5 CIRCUITにおける三相回路図

Fig.6にCIRCUITの設定を示します。外部抵抗，外部インダクタンスは行列として入力します。ソースの数はNO SERIESで設定し，その中で独立な数をPOWER SUPPLIESとします。また，(4)式の接続行列をCONNECTION MATRIXとして設定します。

Fig.6 CIRCUITのinput-1

電圧は(5)式の閉ループの電圧$V_A$、$V_B$を入力値とするため，その求め方を示します。Fig.7に三相対称電圧である枝の電圧$V_1$、$V_2$、$V_3$のベクトルを示します。(5)式より，例えば$V_A$は$V_1$-$V_3$であるから，赤矢印のように大きさが$V_1$の√3倍、位相が$V_1$に比べて30度遅れたベクトルになります。同様に，青矢印で示される$V_B$の大きさは$V_1$の√3倍であり、位相は$V_1$に比べて90度遅れています。従って，Fig.8のように電圧の大きさは100√2Vになる．これは，Y結線をΔ結線に変換し，さらに閉回路とするため一辺を取り除いたV結線に変換しているのと等価となります。なお，大きさに負の符号が付いているのは，NETWORKの定電圧電源の方向の定義が逆になっているためです。

Fig.7 電源の大きさと位相

Fig.8 CIRCUITのinput-2

NETWORKと同様にAC解析を実行し，t=0におけるoutputの回路に関する結果をFig.9に示します。

**************************************************************************** * Step No. 1 Time 0.0000000000e+00 sec * **************************************************************************** *** Sources ********************************************************* ID No. Amplitude(Current) Voltage Flux 1 -3.03498e+00 -8.19080e+01 -1.63184e-02 2 2.94165e+00 4.05665e+01 2.07351e-01 3 9.33253e-02 4.05665e+01 -1.94014e-01 4 0.00000e+00 3.43931e-06 -2.08027e-08 *** Power Sources *************************************************** ID No. Current Voltage 1 -3.03498e+00 -1.22474e+02 2 2.94165e+00 -8.65956e-15 3 0.00000e+00 3.43931e-06

Fig.9のSourcesのID No.1，2，3はそれぞれ枝1，枝2，枝3を表しています。Amplitude (Current)は枝電流 $I_1$，$I_2$，$I_3$，であり，Fig.3のID No.1，2，3の電流に相当します。VoltageはFig.4に示すような各枝の電源以外の電圧降下を表します。例えば，枝1のVoltageはFig.9より-8.19080e+001Vであるが，これはNETWORKのID No.1，5の和に一致していることがわかります。
Fig.9のPower SourcesのID No.1，2はそれぞれ閉ループ A， B を表しています。Currentは閉路電流$I_A$，$I_B$です。VoltageはFig.4に示すような各閉ループの電源を表します。例えば，CIRCUITのID No.1のVoltageは-1.22474e+002Vであるが，これはNETWORKのID No.7，9の和に一致していることがわかります。
三相回路におけるNETWORKとCIRCIUTの関係をご理解いただけたかと思います。CIRCUITの設定方法の説明は，HPに示しておりませんでしたので，NETWORKによる設定方法と比較する形で説明致しました。NETWORKの三相回路の説明は，"Y結線と△結線"にも示しておりますので，参考にして頂ければと思います。NETWORK，CIRCUITのいずれかで設定するにしろ，想定している回路を模擬頂ければと思います。文中でも示しましたが，ここで使用したデータは，CIRCUITは"誘導電動機の解析"，NETWORKによる設定法は，"かご型誘導機の二次元解析におけるロータバーとエンドリングの取り扱い"，"かご型誘導電動機の一極分でのモデル化"にありますので参照して頂ければと思います。