概要

従来、EMSolutionにおきまして軸対称計算を行いますと、中心軸近傍での磁場分布が正常に求まりませんでした。このたび、形状関数の座標系を変換することにより、改良を試みました。今回の改良を施しますと、中心軸付近の分布が滑らかで精度の良いものになっています。

解説

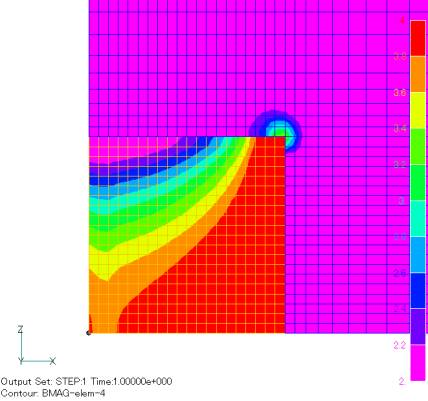
従来、EMSolutionにおきまして軸対称計算を行いますと、中心軸近傍での磁場分布が正常に求まりませんでした。例えば、Fig.1のような円筒磁性体に一様磁場が加わった場合の解析を行いますと、Fig.2のような磁場強度分布が計算されます。 中心付近の磁場分布が不自然なものとなっています。これは、辺要素有限要素法においては、要素が歪みますと、内挿関数がそれに伴って歪むことに起因しています。台形の形の面を貫く磁束を考えますと、短辺側で磁場が強い内挿関数となり、一様な磁場を表現することが困難になります。 EMSolutionにおきましては、２次元軸対称解析では、角度方向に面を拡張します。このため、中心軸付近では、中心側と反対側の辺の長さが大きく異なる要素ができてしまい、このため、磁場計算結果もおかしくなっていました。
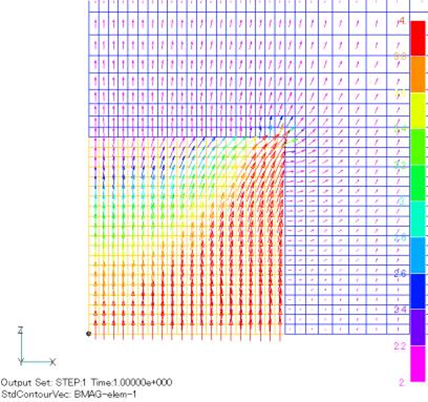
このたび、形状関数の座標系を変換することにより、改良を試みました。磁場強度分布がFig.3のように自然なものとなり、精度が向上したものと思われます。中心軸から離れたところでは、従来の結果とほとんど変わらず、従来のものでも、中心軸付近を気にしなければ正常な分布を示しているものと思われます。

Fig.1 円筒磁性体に一様磁場を
加えた場合の磁束密度分布（改良後）

Fig.2　従来の磁束密度強度分布

Fig.3　改良後の磁束密度強度分布

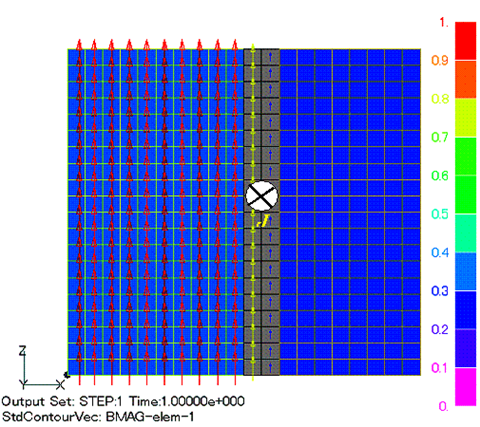
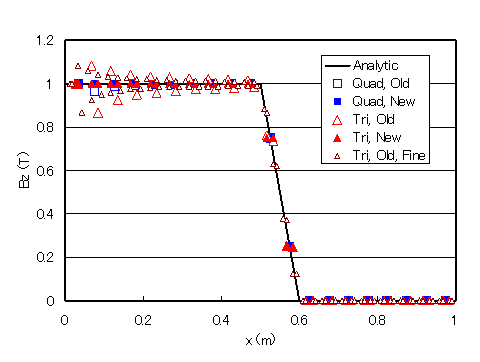
次に非常に単純な場合ですが、無限長ソレノイドコイルの磁場を計算します。Fig.4のようなモデルで、灰色の部分がコイルを表し、中心磁場が１Ｔになるように電流を流しています。 ｚ方向の磁束密度をプロットしますと、Fig.6のようになります。従来のもの(Quad,Old)ではやはり中心軸付近の磁場が理論値から大きくずれますが、今回の改良によるもの(Quad,New)では、理論値に非常に良い精度で一致しています。

Fig.4　無限長ソレノイドコイルの
磁場分布

三角形要素の場合にも、Fig.5に示しますように、従来のままですと中心軸付近の磁場が不自然なものとなります。要素の配列の向きにより、磁束密度の大きさが上下し、径方向で振動しています（Fig.6, Tri, Old）。 この例では、±１０％程度の振動が見られます。この振動は、メッシュを細かくしても同様に現れます。Fig.6, Tri. Old, Fineにメッシュ幅を半分にした場合を示しています。中心からの距離に対して誤差は早く小さくなりますが、振動の幅は変わりません。
今回の改良を施しますと、Fig.6, Tri, Newで示しますように、中心軸付近の分布が滑らかで精度の良いものになっています。メッシュが規則正しいこともありますが、5桁以上の精度で理論解と一致しています。電流が流れているコイルの部分では、磁場は線形に変化するはずですが、線形三角形要素ですとそれを表現することができず、今回の改良の有無に関わらず、階段状の分布となっています。

Fig.5 無限長ソレノイドコイルの
磁場分布
(本改良を含めない三角形要素の場合)

Fig.6 無限長ソレノイドコイルの
ｚ方向磁束密度の理論値との比較