概要

EMSolutionには、磁石の有限要素モデルとしてMAGNETが用意されています。磁石の磁化分布が一様でない場合は、磁石を細分してそれぞれにプロパティを設定し磁化ベクトルを与えるか、または、要素ごと磁化ベクトルを与えます。磁化分布を正弦波の組み合わせで表す正弦関数入力と、数式で表す数式入力により設定する機能について紹介します。

解説

正弦関数入力の対象とする磁化配向は、Fig.1 (a)に示すリング磁石のラジアル配向（円筒座標系における径方向）および(b)に示す平行配向（直交座標系における任意の方向）の二種類があります。数式入力は、任意の磁石形状に対して適用することができます。

(a) ラジアル配向

(b) 平行配向

Fig. 1 リング磁石

以下、正弦関数入力について説明します。このとき、XYZ全体座標系に対し、ラジアル配向に関してはr、θ、z局所座標系を、平行配向に関してはxyz局所直交座標を定義します（Fig. 1）。Fig.1 (a)に示される円筒座標系でのラジアル配向の場合、磁化の径方向（r方向）成分$M_r$の角度方向（θ方向）の分布が(1)式のように正弦関数のフーリエ級数として表されるとします。一般的には、磁化分布が対称となる奇数次高調波が使用されます。

$${\displaystyle M_r(\theta )=M_{rs}\cdot \sum _{k=1,3,5,\cdot \cdot \cdot }^{k_{max}}{b}_k\sin ((\frac{m}{2})k(\theta –{\theta }_0)) (1)}$$

ここで、$M_{rs}$は基準磁化［T］、$k$は高調波次数、$k_{max}$は最大高調波次数、$b_k$はk次の基準磁化により規格化された振幅、$m$は磁極数を表します。角度${\theta }_0$は円筒座標系での基準角度であり、磁化が反転する位置（磁極間）に相当します。$\theta$は円筒座標系での要素中心の角度であり、要素内では磁化は一定とします。 $m$は一周2πに対する極数で、$\frac{m}{2}$は周期数を表します。 Fig. 1 (b)の平行配向の場合は(2)式のように表されます。基準磁化$M_s$は、それぞれの物性領域の局所直交座標で表される定ベクトルとします。$\theta$はx軸からの角度を表します。

$${\displaystyle M(x,y,z)=M_s\cdot \sum _{k=1,3,5,\cdot \cdot \cdot }^{k_{max}}{b}_k\sin ((\frac{m}{2})k(\theta –{\theta }_0)) (2)}$$

例題1として、Fig. 1のモデルに磁化分布を設定した解析を示します。計算条件は、基準磁化$M_s$ =1.0 T、基本波成分のみの最大高調波次数$k_{max}$ =1、その振幅$b_1$=1、極数$m$=4とします。また、磁石の比透磁率は1.02、ヨークの比透磁率は1000、外側は空気としています。Fig.1の配置では、局所座標のx軸方向を全体直交座標のx軸方向とすると、基準角度${\theta }_0$ = $\frac{\pi }{4}$となります。

Fig. 2に、与えられた磁化$M_r$と解析された磁石外側表面の磁束密度$B_r$の波形を示します。ラジアル配向の場合は正弦波に近い磁石外側表面の磁束密度波形が、平行配向の場合は磁極間に歪みのある磁束密度波形となっていることがわかります。また、磁化分布「magnetization」と磁束密度分布「magnetic」をFig. 3に示します。

(i) ラジアル配向

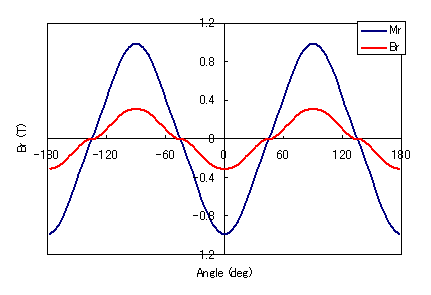
(ii) 平行配向

Fig. 2 最大高調波次数の磁化波形と磁石外側表面での磁束密度波形

(i) ラジアル配向

(ii) 平行配向

(a) 磁化分布 (magnetization)

(i) ラジアル配向

(ii) 平行配向

(b) 磁束密度分布 (magnetic)

Fig. 3 最大高調波次数1の磁化分布と磁束密度分布

次に例題2として、Fig. 1(a)のラジアル配向リング磁石モデルで、$M_{rs}$=1.0T、 $k_{max}$=5、$b_1$=1.0、$b_3$=0.25、$b_5$=0.05とします。Fig. 4に、磁化波形と解析で得られた磁石外側表面の磁束密度波形を示します。高調波成分を含んだ磁化分布にしたがって磁場分布が変わってくることがわかります。

Fig. 4 最大高調波次数5の磁化波形と磁石外側表面での磁束密度波形
（ラジアル配向）