概要

有限要素法では、開領域問題を取り扱うことが難しく、多くの場合外境界を充分に遠くに取り、境界の影響をできるだけ少なくします。しかし、どの程度まで外側に領域を延ばせばよいか、どの程度メッシュを外側に向かって大きくして行くか、等いろいろ頭を悩まされます。また、外側の空気領域のメッシュが多くなり、計算時間や容量が過大になることが考えられます。開領域を扱う一つの方法として、無限境界要素が考えられます。EMSolutionで、その方法を取り入れました。三次元解析では、ICCG法の収束が非常に悪く、実用的か疑問なところもありますが、二次元軸対称問題では充分に使えそうですので、バージョンr7.4よりリリースします。

解説

EMSolutionでは、従来、外境界に対する境界条件として、次の二つの境界条件を使用することができました。

Bn（境界での磁場法線成分）=0

　このとき、At（磁気ベクトルポテンシャルの接線成分）=0の強制条件を境界で課します。

Ht（境界での磁場接線成分）=0

　このとき、Atが自由な自然境界を境界で課します。

境界がトータルポテンシャル領域の時はトータル磁気ベクトルポテンシャルに、変形ポテンシャル領域の時は変形ポテンシャルに対して課します。

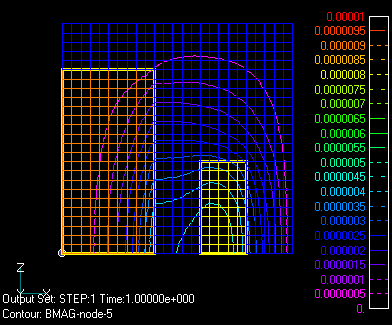
上の二つの条件を課した場合の計算例をFig.1,2に示します。２次元軸対称問題で、中心に鉄コアがあり、外側にコイルが巻かれています。上下は対称としています。図はそれぞれ磁束分布を表しています。磁束は、Bn=0の場合は境界に沿って流れ、Ht=0の場合は境界に直交します。境界の影響を誇張するために境界を近くに取ったため、二つの結果は大きく違っています。Bn=0の場合磁場は小さく、Ht=0のばあい大きく計算されています。これは、多くの場合に当てはまるようです。できれば二つの境界条件で計算を行い、差が小さければ境界の影響は小さく、問題がないと考えられます。

Fig.1　境界でBn=0条件を課した場合（磁束分布）

Fig.2　境界でHt=0条件を課した場合（磁束分布）

さて、同じメッシュで無限境界要素を用いた解析結果をFig.3に示します。これだけではわかりませんが妥当な磁束分布になっています。さらに外側のメッシュを取って、同じように計算した結果をFig.4に示します。Fig.4では、鉄コアおよびコイルの外面を境界としています。Fig.3とFig.4を比べますと、計算領域の磁束分布はほとんど同じになっています。このことは、無限境界要素により、開領域問題が妥当に解けていることを示し、精度的にも問題がないと考えられます。

Fig.3　無限要素境界を使用した場合（磁束分布）

Fig.4　解析領域を小さくし，無限境界要素を使用した場合（磁束分布）

無限境界要素では、境界面要素をFig.5の様に解析領域内の中心点(x0,y0,z0)より放射状に延ばし、無限まで達する要素を考えます。その要素の中で、磁気ベクトルポテンシャルの分布を1/rの多項式で展開します。ｒは中心点からの距離です。展開の次数を大きくすると精度は上がりますが、三次程度で充分なようです。ちなみに上の例では、五次まで取っています。この要素の作り方からわかりますように、外表面は、中心点から延ばした直線が一度だけ交わる形になっている必要があります。そうでない場合は、内部の要素を追加する必要があります。また、並進対称な場合や、平行な面が対称面になる場合は使用できません。

Fig.5　無限境界要素

三次元解析でも使用できますが、ICCG法の収束が極端に悪くなります。小さなモデルでは、適用可能と思われますが、大きなモデルでは実用的では無いように思われます。ICCG法の収束が何故悪くなるかは不明です。 使用する場合は、以下のデータを入力します。他は全く同じです。