概要

並進周期性があって、そのときに外部磁場をLOOP、GCE、ARC等の外部電流ソースで与えるときには、外部磁場も同じ周期性を持つ必要があるため、原理的には電流要素を周期的に無限個入力する必要があります。しかし、実際的には不可能です。このような場合の対応方法について述べます。

解説

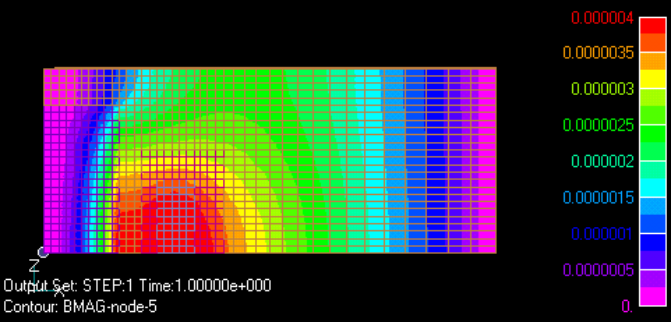
例として、Fig.1の様な二次元軸対称静磁場解析を考えます。中心に鉄コアがあり軸対称コイル（LOOP）で励磁します。このような構造がz方向に等間 隔で並べられているとします。青色と水色の部分は空気とします。解析では上下対称とし、また領域の上側でも対称とします。これらはHt=0 の面となります。空気部分（コイル部分も含めて）は変形ポテンシャル領域とします。実際には無限個のLOOPを定義するのは無理ですので、Fig.2のように、解析領域で周期的においたときと同じ様な磁場になるように、有限個のLOOPを並べます。この例では5個のLOOPを並べています。そのときの解析結果をFig.3に示します。良い結果が得られています。

Fig.1　解析モデル

Fig.2　5個のLOOPを配置したとき

Fig.3　5個のコイルで近似したときの
磁束分布

このような場合の解析法として、もう一つの方法が考えられます。コイルとその周りの空気領域（Fig.1の水色の部分）のみを変形ポテンシャル 領域とし、他の空気部分（濃い青色部分）をトータルポテンシャル領域に変更します。このときはLOOPの入力はFig.1の一つで済みます。境界面は外境界も含めてトータルポテンシャル領域になっている必要があります。ただし、Fig.1の下面は一つのLOOP磁場が対称性を満たしていますので、変形ポテンシャル領域になってもかまいません。LOOP等のビオサバール則による磁場積分はかなり計算時間がかかりますので、このような磁場要素数は小さくする方が有利です。

このようにすれば、対称性の条件はトータルポテンシャルに課せられますので、ソース磁場の非対称性は問題になりません。この結果をFig.4に示 します。Fig.3とほとんど差が認められません。この方法は、コイルが対称面を横切る場合には使用できません。また、コイルはメッシュ領域に含まれてい る必要があります。回転周期性があるときも、同様にして、一周期分のコイル定義で済ませることが可能です。

Fig.4　1個のコイルで周りを
トータルポテンシャル領域としたときの磁束分布